Skip over navigation
How would you work out the area of a circle like this?
You may be curious to find out...
You could download this sheet of circles to play around with some ideas.
Read further to see how others started this challenge...
Raj used a method that he often uses when finding the area of shapes:
Fran tried a different idea:
Jay tried cutting up the circle:
Michelle had another idea:
What do you think about each of these four ways of finding the area of a circle?
Which do you think is 'best' and why?
Do let us know about any other methods that you devise too.
Circular Area
Age 7 to 11
Challenge Level 
How would you work out the area of a circle like this?
You may be curious to find out...
You could download this sheet of circles to play around with some ideas.
Read further to see how others started this challenge...
Raj used a method that he often uses when finding the area of shapes:
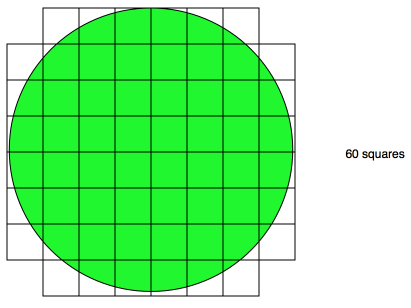
He put a square grid over the circle. He counted 60 squares but then he had to decide what to do when the squares were not completly over the circle.
Fran tried a different idea:
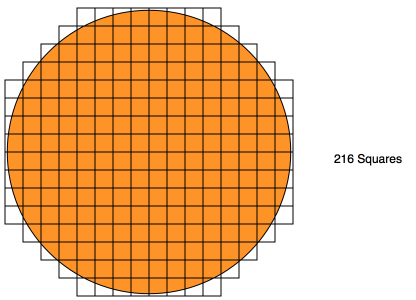
Fran used smaller squares than Raj. She used 216 but she noticed that some of the squares overlapped the circle at the edge.
Jay tried cutting up the circle:
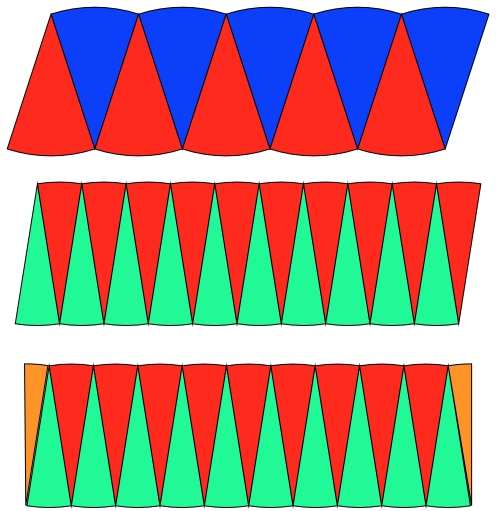
Jay cut across the circle going through the centre. He coloured the segments to make them easier to see, then put them together:
Michelle had another idea:
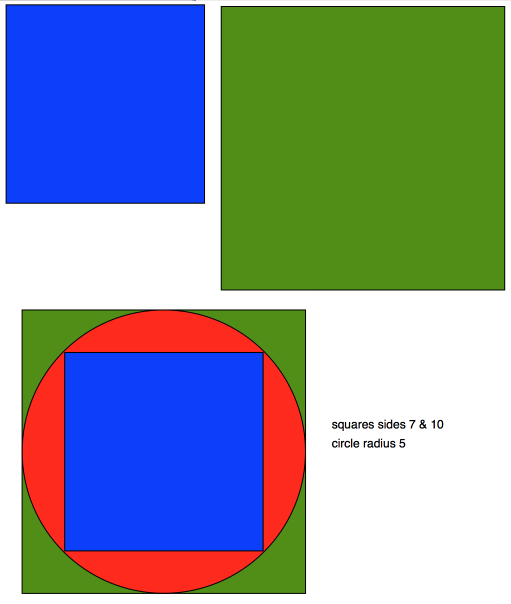
She made a square that just fits inside the circle and a larger one that just enclosed the circle. She worked out the area of each square and then took the average.
What do you think about each of these four ways of finding the area of a circle?
Which do you think is 'best' and why?
Do let us know about any other methods that you devise too.