Skip over navigation
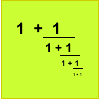

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Proof Sorter - the Square Root of 2 Is Irrational
Age 16 to 18
Challenge Level 





- Interactive environment
Perhaps you might like to try generalising this proof to prove that $\sqrt n$ is irrational when $n$ is not a square number.
Now $(1.4)^2=1.96$, so the number $\sqrt 2$ is roughly $1.4$. To get a better approximation divide $2$ by $1.4$ giving about $1.428$, and take the average of $1.4$ and $1.428$ to get $1.414$. Repeating this process, $2\div 1.414 \approx 1.41443$ so $2\approx 1.414 \times 1.41443$, and the average of these gives the next approximation $1.414215$. We can continue this process indefinitely,
getting better approximations, but never finding the square root exactly.
If $\sqrt 2$ were a rational number, that is if it could be written as a fraction $p/q$ where $p$ and $q$ are integers, then we could find the exact value. The proof sorter shows that this number is IRRATIONAL so we cannot find an exact value.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Rational Roots
Given that a, b and c are natural numbers show that if sqrt a+sqrt b is rational then it is a natural number. Extend this to 3 variables.

