What Does it All Add up To?

Tobias from Wilson's School sent in this diagrammatic proof that the sum of four consecutive numbers can never be a multiple of 4:

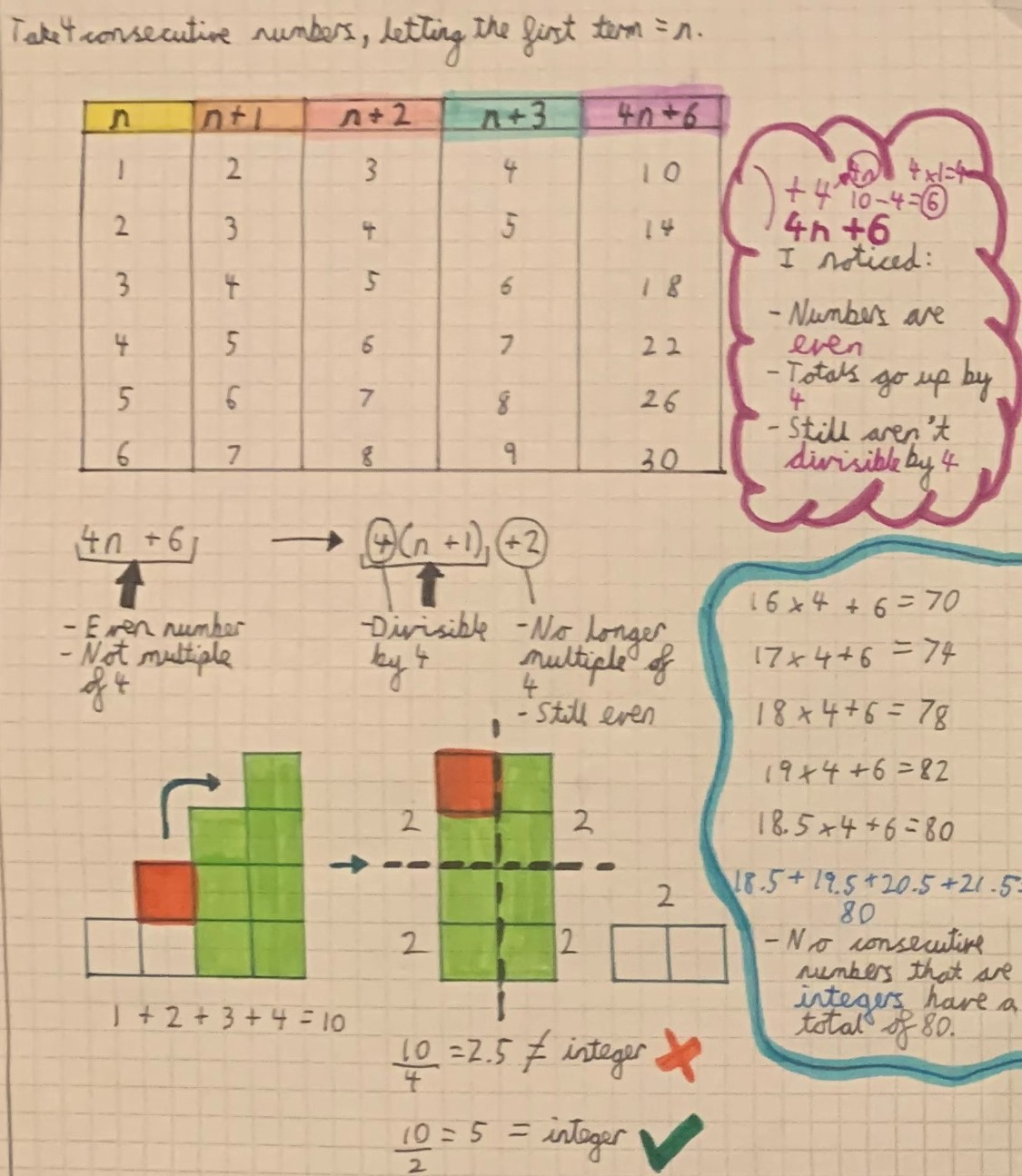
Shayen from Wilson's School in England investigated the sums of 5 consecutive numbers. Here is Shayen's work (click to see a larger version):

Tobias sent in this diagrammatic proof that what Shayen noticed is always true:

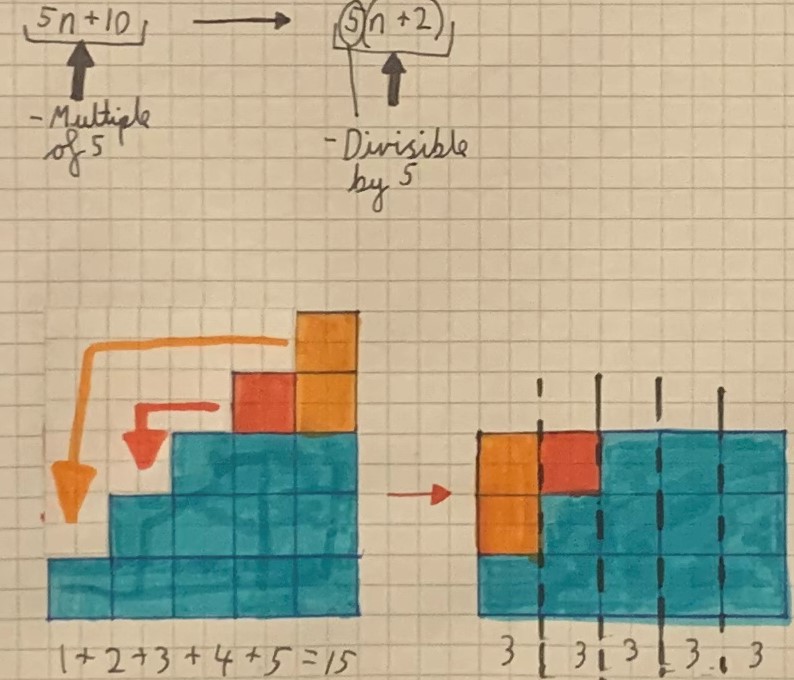
Sunhari from British School Muscat and Mahdi from Mahatma Gandhi International School in India sent in this algebraic proof:

Let the five consecutive numbers be $n, n+1, n+2, n+3, n+4$
$\begin{split}n+n+1+n+2+n+3+n+4 & =5n+10\\
&=5(n+2)\\
&=5a for a = n+2\end{split}$

Shayen also investigated the sums of 6 consecutive numbers. Here is Shayen's work (click to see a larger version):

Here is Tobias's diagrammatic proof of what Shayen noticed:

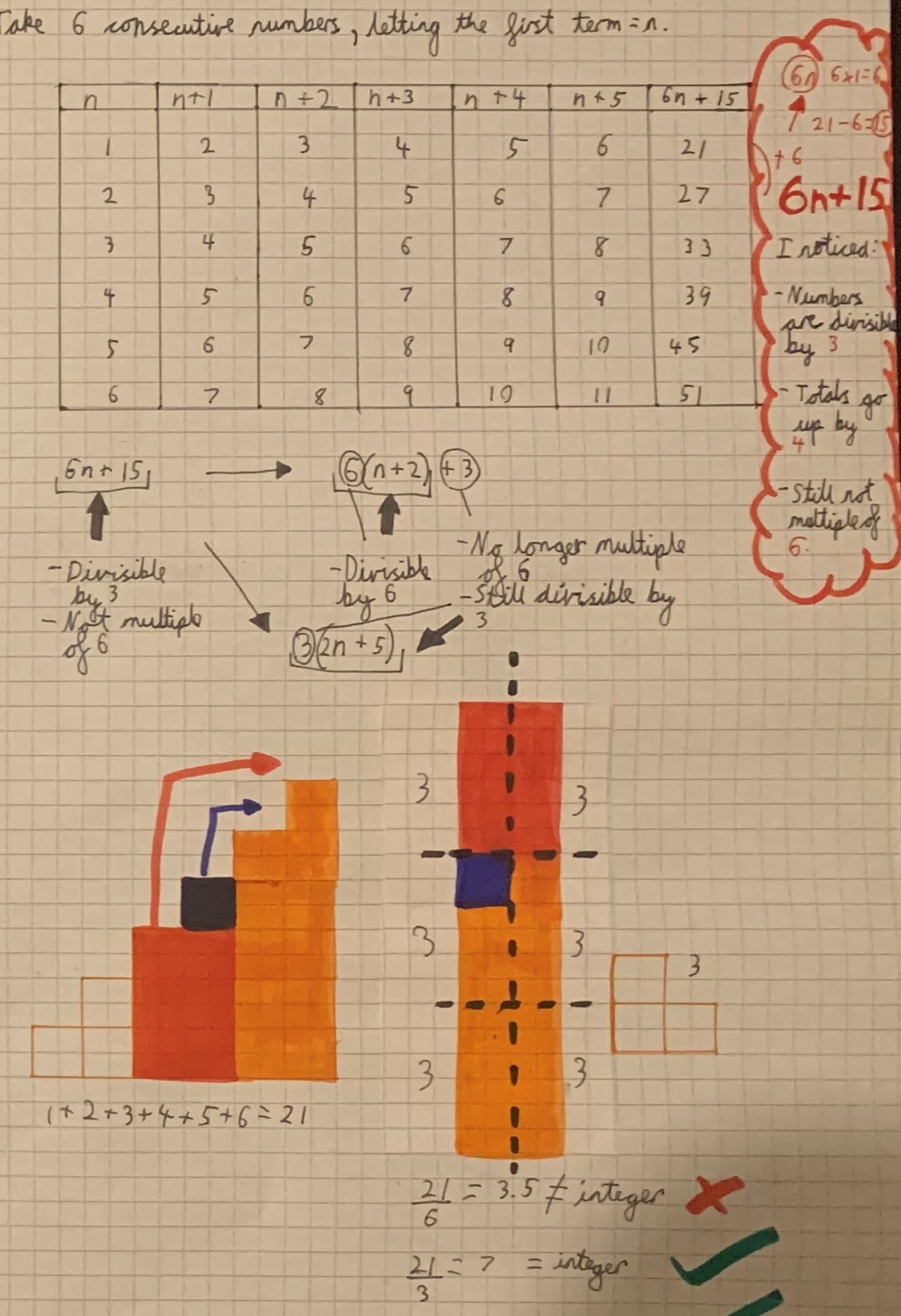
Here is Mahdi and Sunhari's algebraic proof:

Let the six consecutive numbers be $n, n+1, n+2, n+3, n+4, n+5$
$\begin{split}n+n+1+n+2+n+3+n+4+n+5&= 6n + 15\\&= 3(2n+5)\end{split}$
It is an odd multiple of 3, and cannot be factorised to a multiple of six.

Shayen made a conjecture about adding other numbers of consecutive numbers (click to see a larger version):

Egeman from Wilson's School represented this algebraically:

Let $a$ be the first number in a sequence of consecutive numbers
Let $n$ be the number of numbers in a sequence of consecutive numbers
Let $s$ be the sum of the numbers in a sequence of consecutive numbers

where $n=1, s=1a+0$;
where $n=2, s=2a+1$;
where $n=3, s=3a+3$;
where $n=4, s=4a+6$;
where $n=5, s=5a+10$;
where $n=6, s=6a+15$; etc

$s$ consists of two parts: a multiple of $a$ and a triangle number.
The multiple of $a$ is always $na$.
The triangle number is the $(n-1)^\text{th}$ term in the sequence of triangle numbers.

Mahdi and Sunhari showed why $s$ takes this form. This is Mahdi's work:

From here, Mahdi, Sunhari and Egeman all used a formula for the $(n-1)^\text{th}$ triangular number to show that if $n$ is odd, $s$ is a multiple of $n$, and if $n$ is even, then $s$ is not a multiple of $n$ but is a multiple of $\frac n2.$ Here is Mahdi's work: