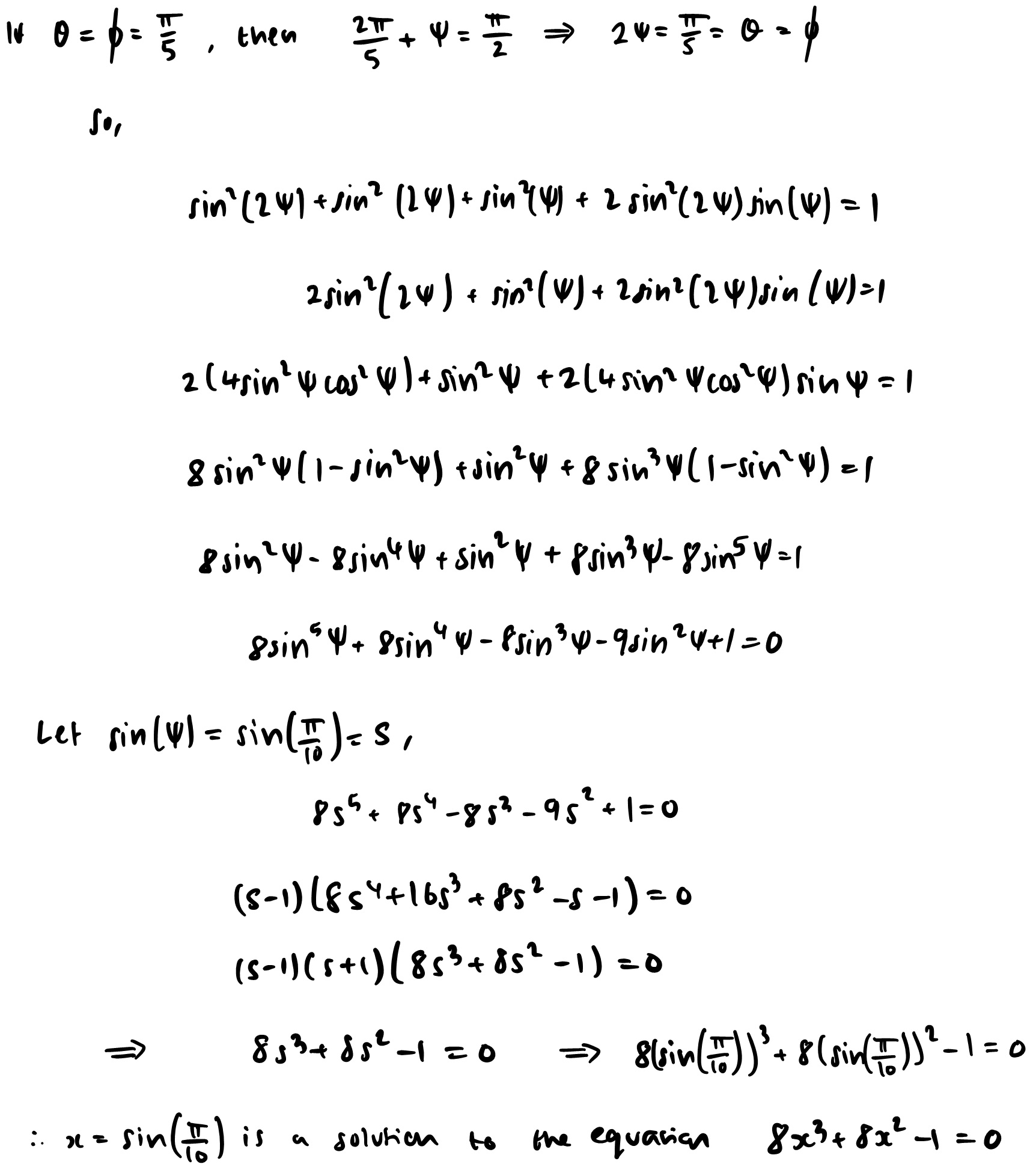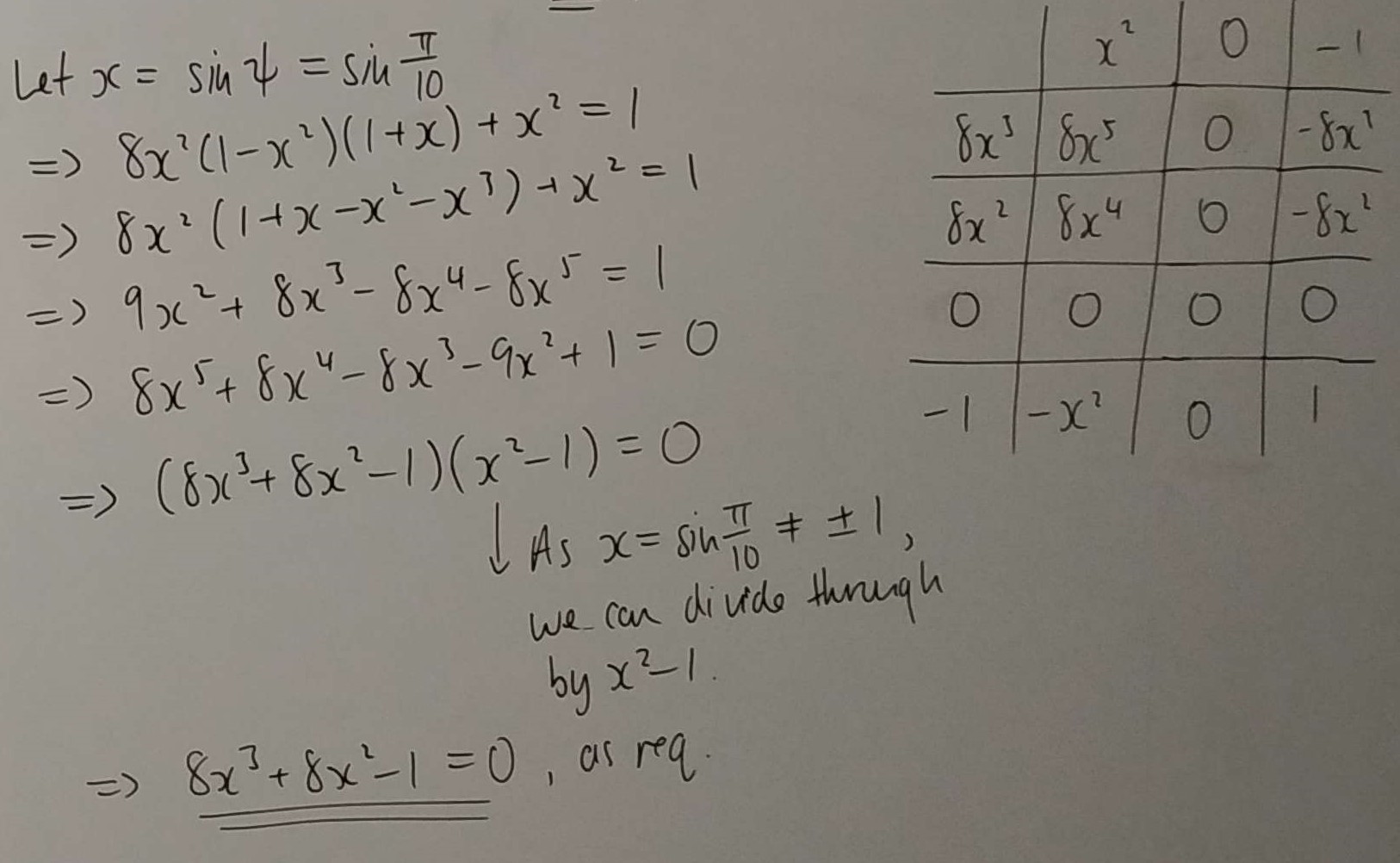Tri-angled Trig

Show that $\sin\theta+\sin\phi+\sin\psi=1$

Leo from Stowe School, Edward from Sir William Robertson Academy and James from St Bernards all began from $\sin{(\theta+\phi+\psi)}=1.$ This is James's work (click on the image to open a larger version):

Joshua from Bohunt Sixth Form and Dylan from Brooke Weston used the substitution $\psi=\frac\pi2-\theta-\phi.$ This is Dylan's work (click on the image to open a larger version):

Dibyadeep from Greenhill School in the USA split the sines up in a different way, and wrote up the results in the format of a paper. Click here to download Dibyadeep's paper, which also includes the second part of the problem.

Show that $\sin{\frac\pi{10}}$ satisfies the equation $8x^3+8x^2-1=0$

Leo, Joshua, Dylan, James and Edward all solved the second part of the problem by substituting $\sin\frac\pi{10}$ as $x$ (or $s$), expanding and factorising. Leo and Dylan factorised by inspection. Here is Leo's work:

Dylan was a bit more explicit about the facotrising. Click to see some of Dylan's work.

Joshua, James and Edward used the factor theorem, and Edward used polynomial long division to factorise the quintic. Here is some of Edward's work:

Dibyadeep didn't need to factorise at all, because at this point in Dibyadeep's working, $1-x^2$ was written as $\cos^2\frac\pi{10}.$ Click here to download Dibyadeep's paper.