The Matrix

A Matrix is a rectangular array of numbers (which are called the entries of the matrix).  The plural of matrix is matrices.

The matrix $
\begin{pmatrix}2&-3&\phantom{-}5\\0&\phantom{-}8&-1\end{pmatrix} $ has two rows and three columns.  We say that the dimension of the matrix is $2 \times 3$.

You can add and multiply two matrices if they satisfy certain conditions. To add two matrices they must have the same dimensions, and then you can add together the corresponding elements.

Example:
$$
\begin{pmatrix}\phantom{-}2&\phantom{-}0\\\phantom{-}9&-3\\\phantom{-}1&\phantom{-}4\end{pmatrix}+\begin{pmatrix}-5&\phantom{-}1\\\phantom{-}2&\phantom{-}3\\\phantom{-}0&-1\end{pmatrix}=\begin{pmatrix}2+ -5&\phantom{-}0+1\\9+2&-3+3\\1+0&\phantom{-}4+-1\end{pmatrix}=\begin{pmatrix}-3&\phantom{-}1\\\,11&\phantom{-}0\\\phantom{-}1&\phantom{-}3\end{pmatrix}
$$

To multiply two matrices together then the number of columns of the first matrix has to be equal to the number of rows of the second matrix.  The example below shows how one element of the product of two matrices has been calculated - can you see how the other elements have been generated?

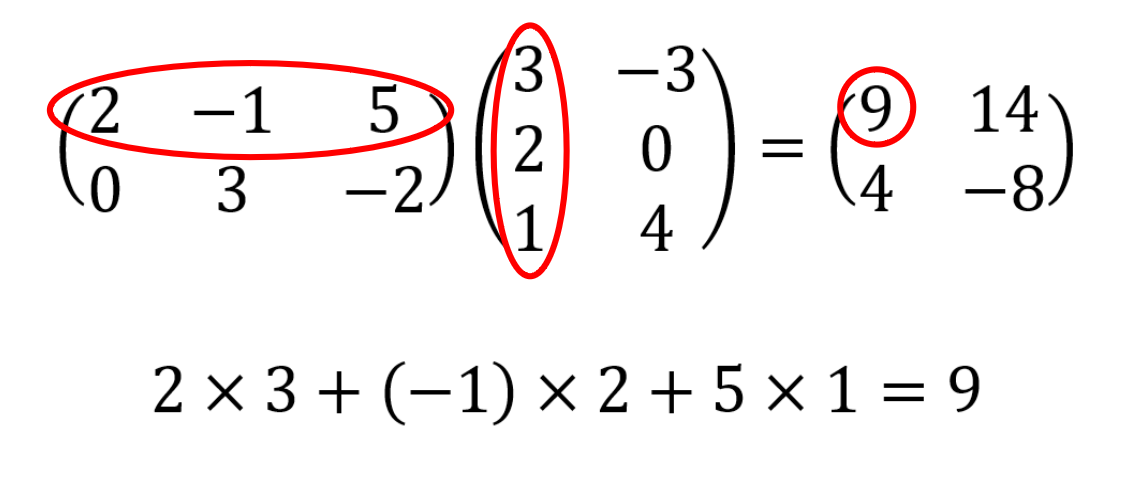
You can use this matrix to check how the other elements were calculated.  If you click on entries in the answer matrix you will see the relevant rows and columns highlighted and the calculations used to generate the entry.

Calculate these matrix products:

1. $\begin{pmatrix}3&-3\\2&0\\1&4\end{pmatrix} \begin{pmatrix}2&-1&5\\0&3&-2\end{pmatrix}$
    
2. $\begin{pmatrix}2&-1\\3&5\end{pmatrix}\begin{pmatrix}5&-3\\-1&0\end{pmatrix}$
    
3. Let ${\bf P}=\begin{pmatrix}2&3&-1\end{pmatrix}$ and let ${\bf Q}=\begin{pmatrix}-1\\0\\5\end{pmatrix}$.  Find the products ${\bf P}{\bf Q}$ and ${\bf Q}{\bf P}$.
    
4. Let ${\bf A} = \begin{pmatrix}3&-1&0\\-2&5&1\end{pmatrix}$ and ${\bf B}=\begin{pmatrix}3&2 \\ 0 & -1\end{pmatrix}$.  State which of the products ${\bf A}{\bf B}$ and ${\bf B}{\bf A}$ can be calculated and find this product.

You might like to use this Matrix Multiplication Calculator to check your answers.  If you click on an entry in the answer matrix you can see how the value was calculated.

For the rest of this question we will consider square $2 \times 2$ matrices, so matrices of the form $\begin{pmatrix}a&b\\c&d\end{pmatrix}$.  Here are some questions to think about:

1. With numbers it does not matter which order we use to multiply, so $2 \times 3 = 3 \times 2$.  Is the same true of matrices, i.e. do we have ${\bf A}{\bf B} = {\bf B}{\bf A}$ in all cases?
    
2. If ${\bf A}{\bf B}={\bf 0}$, must we have at least one of ${\bf A}$ or ${\bf B}$ equal to ${\bf 0}=\begin{pmatrix}0&0\\0&0\end{pmatrix}$?
    
3. Consider the matrix ${\bf M}=\begin{pmatrix}0&-1\\1&0\end{pmatrix}$.  What is the matrix ${\bf M}^{2023}$?
    
4. The $2 \times 2$ matrix ${\bf P}$  satisfies ${\bf P}{\bf X} = {\bf X}{\bf P}$ for all possible $2 \times 2$ matrices ${\bf X}$. Find the possible matrices that ${\bf P}$ could be.
   
    
   You could write ${\bf P} = \begin{pmatrix}a&b\\c&d\end{pmatrix}$. The equation works for all possible ${\bf X}$, so you can try using a simple specific matrix ${\bf X}$ and see what you can deduce about ${\bf P}$. Then try another matrix ${\bf X}$ to see if you can deduce something else!

There are more matrix problems in this feature.