Skip over navigation
Bound to Be
Age 14 to 16
Challenge Level 
 |
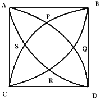
$ABCD$ is a square of side 1 unit.
Arc of circles with centres at $A, B, C, D$ are drawn in.
Prove that the area of the central region bounded by the four arcs is: $(1 + \pi/3 + \sqrt{3})$ square units. |
You may also like
Giant Holly Leaf
Find the perimeter and area of a holly leaf that will not lie flat (it has negative curvature with 'circles' having circumference greater than 2πr).
Quadarc
Given a square ABCD of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The four arcs intersect at P, Q, R and S. Find the area enclosed by PQRS.
Get Cross
A white cross is placed symmetrically in a red disc with the central square of side length sqrt 2 and the arms of the cross of length 1 unit. What is the area of the disc still showing?