Shear Magic

Why do this problem?

Many students have only a superficial understanding of the formula for the area of a triangle, particularly when they move away from right angled triangles. This problem starts with an exploration of shearing parallelograms and then encourages students to think of a triangle as half a parallelogram, which should lead to a more secure understanding of where the triangle formula comes from, and a better appreciation of how areas change or remain the same as we transform shapes.

Possible approach

Start by showing students these two images and inviting them to jot down anything they notice:

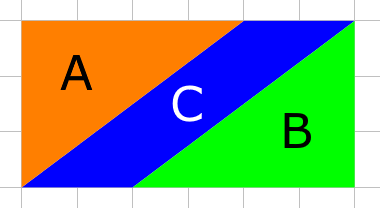
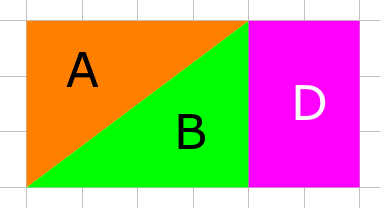
You could pose the question "Which area is bigger, C or D? How do you know?" and give students time to come up with a justification for why we know C and D must have the same area. 

Then share these two images:

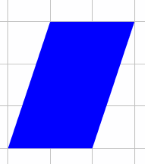
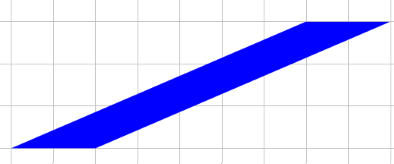
Invite students to draw similar diagrams to find the area of these two parallelograms.
"I wonder if all parallelograms with base 2 and height 3 will have the same area..." Students could explore using pencil and squared paper. When they are ready, they can move on to explore other bases and heights, perhaps using the first interactivity in the problem.

Once students have had time to explore, bring the class together to develop a formula for the area of a parallelogram based on their findings.
If appropriate, introduce the word "shear" to describe this type of transformation - a suggested definition is included in the notes and background section at the bottom of the problem.

Next, share this image of a family of triangles:

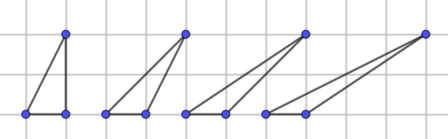
"How can we use what we found out about parallelograms to help us find the area of these triangles?"
Again, students can explore using pencil and squared paper, or using the second interactivity in the problem.

Once students have had time to explore, bring the class together to develop a formula for the area of a triangle based on their findings. The interactivities could be used to test out the formula, by creating a triangle and then inviting students to predict what the area is before clicking "Show area".

Key questions

Which areas are the same?
How do you know?
How does the area of the triangle compare with the area of the parallelogram?

Possible support

Show some examples using the interactivities, and then encourage students to draw the diagrams for themselves on squared paper, paying particular attention to drawing the correct parallelogram for a given triangle.

Invite students to predict what will happen if the red dot moves one unit to the right, or if the green dot moves 1 unit up. Then take time to explore those patterns, recording them using squared paper.

For some students, cutting out the shapes in the first part of the problem may help them to see the conservation of area.

Possible extension

Students could use what they have learned about areas of triangles to explore Isosceles Triangles.