Cut Nets
The net of a cube has been cut into two. It could be put together in several ways so that it could be folded into a cube.
Here are the nets of $9$ solid shapes. Each one of these has been cut into $2$ pieces, like the net of the cube.
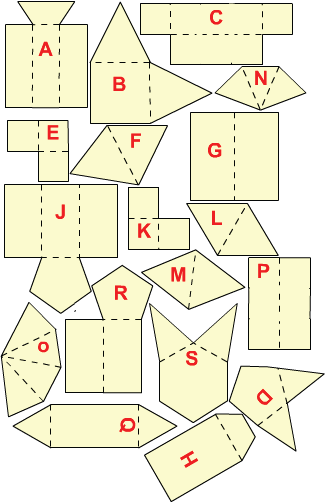
Can you see which pieces go together?
You may also like
Tetrahedron Faces
One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Redblue
Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?