Skip over navigation
Hallie and Moira from Southbury Elementary in the US sent us the following:
When solving this problem, we found it easiest to look for similarities between the nets. One of the most obvious pairs were nets 'e' and 'k' because they are the same shape, each with 3 squares of the same size, so you could infer that when folded into their 3-D forms they will form a cube.
Another easier one was 'c' and 'p', because they have rectangles that have the same dimensions as each other. You could use this strategy (looking for equivalent dimensions) for other pairs too such as 'b' and 'f', 'l'and 'm', 'n' and 'd', and 'o' and 's'.
For sets like 'r' and 'j', 'h' and 'a' and 'g' and 'q', you find more similarity between the regular polygons such as the pair of trapezoids or hexagons. We also find it interesting that about
half of the nine figures are pyramid shapes and about half are prisms. We found it helpful to make a list and use process of elimination. We also cut out the shapes and folded and taped them to check our answers:

Brandon and Rebecca from Oakwood Academy send in the following picture:

This is what their teacher wrote:
Two of our pupils at our SEN school have done really well with this challenge. They were given some support due to the nature of their learning needs.
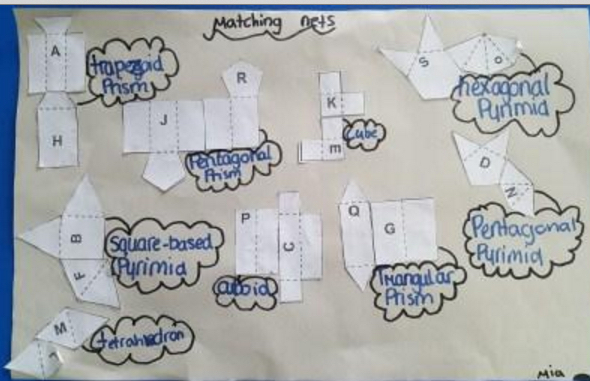
Mia and IsabelleӬ, from Fordingbridge Junior School, wroteӬ
First we looked for similar 2D shapes and gently folded them to see if they created one of the finished 3D shapes. Then if it worked we would experiment to find out how the net would be put together. If it didn't work we would choose another piece of net with similar 2D shapes until we
found one that worked.
With the last few shapes we looked at how many sides the main shape, like a square, hexagon, pentagon or trapezium had and found another piece of net that could cover all of the sides. For example to find out that A and H worked we looked for two pieces with trapeziums on. Then we gently folded them together and it formed a 3D shape.
We also had a number of solutions sent in from Cromer Junior School; namely Amy and Grace, Jacob, Owen and Ashley, Glen and Toby, Noah, Shannon, Aleesha and Brandon. Thank you for your good solutions.
Finally, Mr ArnoldӬ from The Gerrards Cross C of E SchoolӬ wrote:
Hi there. My class really loved working on Cut Nets. The attached file contains workings, reasoning and explanations on what they found, which they wrote themselves in small groups.
The Gerrards Cross C of E School.docx or The Gerrards Cross C of E School.pdf
Thank you everyone who sent in a solution. Keep up the good work and please send in further solutions to future live problems!


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cut Nets
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Hallie and Moira from Southbury Elementary in the US sent us the following:
When solving this problem, we found it easiest to look for similarities between the nets. One of the most obvious pairs were nets 'e' and 'k' because they are the same shape, each with 3 squares of the same size, so you could infer that when folded into their 3-D forms they will form a cube.
Another easier one was 'c' and 'p', because they have rectangles that have the same dimensions as each other. You could use this strategy (looking for equivalent dimensions) for other pairs too such as 'b' and 'f', 'l'and 'm', 'n' and 'd', and 'o' and 's'.
For sets like 'r' and 'j', 'h' and 'a' and 'g' and 'q', you find more similarity between the regular polygons such as the pair of trapezoids or hexagons. We also find it interesting that about
half of the nine figures are pyramid shapes and about half are prisms. We found it helpful to make a list and use process of elimination. We also cut out the shapes and folded and taped them to check our answers:

Brandon and Rebecca from Oakwood Academy send in the following picture:

This is what their teacher wrote:
Two of our pupils at our SEN school have done really well with this challenge. They were given some support due to the nature of their learning needs.
Mia and IsabelleӬ, from Fordingbridge Junior School, wroteӬ
First we looked for similar 2D shapes and gently folded them to see if they created one of the finished 3D shapes. Then if it worked we would experiment to find out how the net would be put together. If it didn't work we would choose another piece of net with similar 2D shapes until we
found one that worked.
With the last few shapes we looked at how many sides the main shape, like a square, hexagon, pentagon or trapezium had and found another piece of net that could cover all of the sides. For example to find out that A and H worked we looked for two pieces with trapeziums on. Then we gently folded them together and it formed a 3D shape.

We also had a number of solutions sent in from Cromer Junior School; namely Amy and Grace, Jacob, Owen and Ashley, Glen and Toby, Noah, Shannon, Aleesha and Brandon. Thank you for your good solutions.
Finally, Mr ArnoldӬ from The Gerrards Cross C of E SchoolӬ wrote:
Hi there. My class really loved working on Cut Nets. The attached file contains workings, reasoning and explanations on what they found, which they wrote themselves in small groups.
The Gerrards Cross C of E School.docx or The Gerrards Cross C of E School.pdf
Thank you everyone who sent in a solution. Keep up the good work and please send in further solutions to future live problems!
You may also like
Tetrahedron Faces
One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Redblue
Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?

