A Chain of Eight Polyhedra
These two 3-D shapes, the tetrahedron and the octahedron have the same 2-D shape, an equilateral triangle, as their faces.
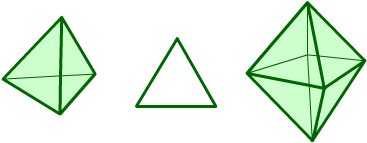
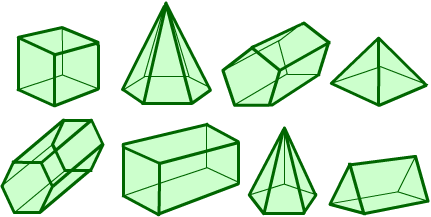
Can you arrange the shapes below in a chain so that each one shares a face (or faces) that are the same shape as the one that follows it? (The faces do not have to be the same size.)
You may also like
Tetrahedron Faces
One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Redblue
Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?