Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
A Chain of Eight Polyhedra



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A Chain of Eight Polyhedra
These two 3-D shapes, the tetrahedron and the octahedron have the same 2-D shape, an equilateral triangle, as their faces.
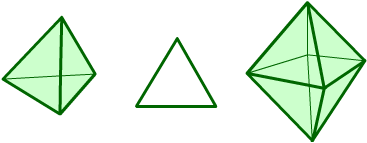
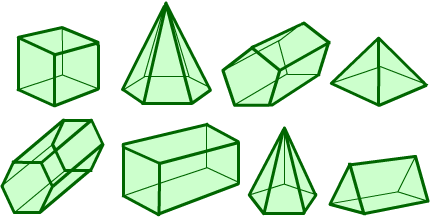
Can you arrange the shapes below in a chain so that each one shares a face (or faces) that are the same shape as the one that follows it? (The faces do not have to be the same size.)
Why do this problem?
Key questions
Possible extension
Learners could add some more 3D shapes and try to make a longer chain. Perhaps they could draw the shapes as in the problem.Possible support
Suggest using these cards and listing some of the shapes of their faces. This list of faces that are given in the hints might be helpful.You may also like
Tetrahedron Faces
One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Redblue
Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?

