A Chain of Eight Polyhedra
Many of you sent solutions to this problem, although none of you tried to find more than one way of making a chain. Wilson from Beecroft Primary School sent in a diagram which shows one chain very clearly. In fact Wilson noticed that this is a loop, not just a chain:
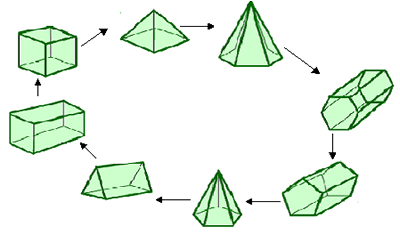
Rachael, Chloe and Emilia from Ardingly College Junior School found a different chain:
Hexagonal prism
Hexagonal based pyramid
Pentagonal based
pyramid
Pentagonal prism
Cuboid
Cube
Square based
pyramid
Triangular prism
Zara, also from Ardingly College Junior School discovered another chain:
Triangular prism - Square based pyramid - cube - cuboid - pentagonal
prism - hexagonal prism - hexagonal based pyramid - pentagonal based
pyramid.
The links between these eight shapes are that between the
triangular prism and square based pyramid are the triangle. Next the
link is the square, then the square again. Between the cuboid and
pentagonal prism is the rectangle. Next the link is rectangle again then
the hexagon. Last of all the link is the triangle.
Do these make loops too?
Alex and Katie from Woodfall Junior
described how the links worked in their loop:
Cube connects to the cuboid by a square.
Cuboid connects to the
hexagonal prism by a rectangle.
Hexagonal prism connects to the
hexagonal based pyramid by a hexagon.
Hexagonal based pyramid
connects to the pentagonal based pyramid by an isoceles triangle.
Pentagonal based pyramid connects to the pentagonal prism by a pentagon.
Pentagonal prism connects to the triangular prism by a rectangle.
Triangular prism connects to the square based pyramid by an equilateral
triangle.
Square based pyramid connects to the cube by a square.
Then we asked you how many different ways there are to make a loop.
Danny, aged 11, explained how he went about it:
I made a table of what types of faces each shape has, and then worked out from that which shapes can go next to each other.|
| Square face | Hexagon face | Triangle face | Pentagon face | Rectangle face |
| Cube | Yes | No | No | No | No |
| Hexagon-based pyramid | No | Yes | Yes | No | No |
| Pentagonal prism | No | No | No | Yes | Yes |
| Square-based pyramid | Yes | No | Yes | No | No |
| Hexagonal prism | No | Yes | No | No | Yes |
| Cuboid | Yes | No | No | No | Yes |
| Pentagon-based pyramid | No | No | Yes | Yes | No |
| Trianglar prism | No | No | Yes | No | Yes |
| Shape | Goes with |
| Cube | Square-based pyramid, Cuboid |
| Hexagon-based pyramid | Hexagonal prism,Square-based pyramid,Pentagon-based pyramid,Trianglar prism |
| Pentagonal prism | Pentagon-based pyramid, Hexagonal prism, Cuboid, Trianglar prism |
| Square-based pyramid | Cube, Cuboid, Hexagon-based pyramid,Pentagon-based pyramid, Trianglar prism |
| Hexagonal prism | Hexagon-based pyramid, Pentagonal prism, Cuboid, Trianglar prism |
| Cuboid | Cube, Square-based pyramid,Pentagonal prism,Hexagonal prism,Trianglar prism |
| Pentagon-based pyramid | Pentagonal prism, Hexagon-based pyramid,Square-based pyramid,Trianglar prism |
| Trianglar prism | Hexagon-based pyramid ,Square-based pyramid,Pentagon-based pyramid,Pentagonal prism,Hexagonal prism,Cuboid |
You may also like
Tetrahedron Faces
One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.
Redblue
Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?