All Tied Up
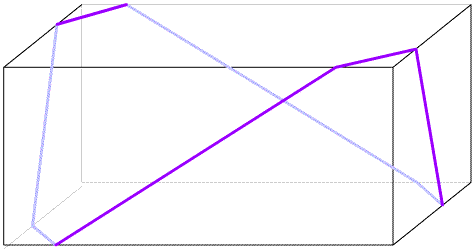
I like to run a ribbon around the box so that it makes a complete loop with two parallel pieces of ribbon on the top (and on the bottom) of the box.
The ribbon crosses every face once, except the top and bottom, which it crosses twice.
The ribbon rests tightly against the box all the way round because the angle at which it meets a corner is continued onto the next face.
I can cut the ribbon in advance of placing it around the box and I can slide the ribbon around a little to position it.
If the box is $20 \text{ cm}$ by $10 \text{ cm}$ by $5 \text{cm}$ - how long will the ribbon be?
Show why it is possible for me to "slide" the ribbon.
What will it be for any box with height $h$, width $w$ and length $l$? (n.b. the length and width are the longer distances and form the top of the box. Would the string be longer or shorter if this was not the case?)
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?