Maximum Flow

Yanqing from Lipson Community College and Andrei from Tudor Vianu National College, Bucharest, Romania both sent correct solutions.

Andrei wrote:

" As I am not familiar with graph theory, I first read the hint and the notes of the problem, then I looked on the web for the Maximum flow, minimum cut theorem. I found different examples, algorithms of solving such problems, as well a possible list of utilisation.

I started with the definition of terms: a cut in a network is a minimal set of edges whose removal separates the network into two components, one containing the source, and the other the sink."

In the first network a cut through $PT$, $RT$, $RU$, $RB$, and $SB$ separates the network showing that the flow cannot be more than $18$ units (the total flow through these edges).

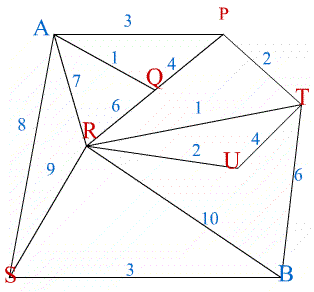
This flow is possible by sending: $3$ units along $ASB$, $5$ units along $ASRB$, $5$ units along $ARB$, $2$ units along $ARUTB$, $1$ unit along $AQRTB$ and $2$ units along $APTB$. Hence the maximum flow is $18$ units.

In the second network a cut through $BC$, $DC$, $FG$ and $HG$ separates the network so the flow cannot be more than $16$ units (the total flow along these edges).

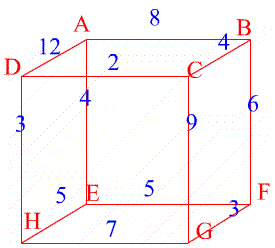
This flow is possible by sending $3$ units along $ABFG$, $4$ units along $ABCG$, $2$ units along $ADCG$, $3$ units along $ADHG$ and $4$ units along $AEHG$. Hence the maximum flow is $16$ units.