Eureka!

In 322 BC, Alexander the Great built the city of Alexandria and soon afterwards, under the reign of Ptolemy, it became the capital of Egypt. To attract clever people to this city, Ptolemy set up a university in Alexandria, which was the first of its kind. It was at the University of Alexandria that nearly all the famous mathematicians of the time studied or taught.


Archimedes was one of these. He was born in about 287 BC in the city of Syracuse on the island of Sicily. We think that Archimedes visited Alexandria and studied there, as he seems to have had many friends who were also great mathematicians.

Archimedes on a Greek stamp

This image was taken from the following website: http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Archimedes.html

There are many stories about Archimedes' discoveries and inventions. When the Romans were attacking Syracuse, the King (who was also a good friend) asked Archimedes to help defend the city. He invented huge cranes, which could lift ships out of water; movable poles which dropped weights on enemy ships and powerful catapults.

Archimedes' Claw, a device which lifted ships into the air and rolled them over.

www.mcs.drexel.edu/~crorres/Archimedes/Claw/illustrations.html (unfortunately this link is no longer active)

Archimedes also developed complicated pulley systems to drag ships along. These war-time inventions gained Archimedes a lot of recognition and respect from the local people.

It was when Archimedes was in his bath that he jumped up shouting the famous "Eureka!" He had been trying to solve a problem for the King - how to find out whether the King's crown was pure gold or if some silver had been added. As he got into the bath, some water sloshed over the sides and this inspired Archimedes to try an experiment. He discovered that when the crown was put in a bowl of water, more water over-flowed than when the same weight of pure gold was put in. This meant that the crown could not be entirely pure gold. This led to the first law of hydrostatics. You can find out about this in more detail on the websites listed at the end.

Although Archimedes became famous for his inventions during the war, he loved to study "pure" maths much more. He had a passion for geometry and he wrote many important papers on different topics. Here we shall concentrate on his spiral.

Archimedes' Spiral

A spiral is a special kind of curved path on a 2d (flat) surface. Spirals are described in maths by sets of equations and are given different names. Archimedes investigated many different types of spirals and one of these is now named after him.

The Archimedes' spiral is the path of a point that is travelling towards or away from a fixed origin at a constant speed and constant velocity . Velocity is a measure of speed in a particular direction.

This is what it looks like:

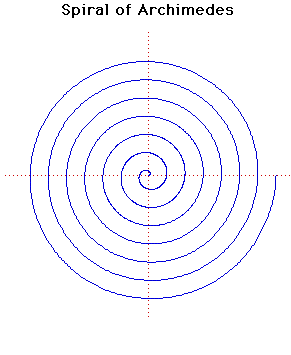
www-groups.dcs.st-andrews.ac.uk/~history/Curves/Spiral.html

As if all this wasn't enough, Archimedes investigated many other branches of geometry. One of his most famous proofs was the calculation of pi to between 3 10/71 and 3 1/7. (See Pi, AVery Special Number )

It is said that Archimedes used to get very absorbed in his work and would draw diagrams in sand, ashes from the fire and even on himself using bathing oils! One story tells that it was due to this total absorption in maths that Archimedes was killed. Apparently, he asked a Roman soldier to stand out of the way of a diagram he had sketched in the sand. The soldier ran a spear through his chest.

This Roman floor mosaic shows Archimedes' death


http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Archimedes.html






Archimedes can be regarded as one of the most accomplished mathematicians in history. His discoveries certainly seem remarkable, considering how long ago he lived. We've only touched the surface here so if you'd like to read more about him, why not take a look at some of the websites listed below? Go on...

www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Archimedes.html

www-maths.mcs.st-andrews.ac.uk/~gmp/gmpANA.html

physics.weber.edu/carroll/Archimedes/theIndex.htm

There is also a lot of information about Archimedes in "An Introduction to the History of Mathematics" (4th edition) by Howard Eves published by Holt, Rinehart and Winston.