Skip over navigation
Curt from Reigate College started by getting a general formula for Triangle numbers
$T_n = 1 + 2 + 3+ . . . +(n-1) + n$
$T_n = n + (n-1) + . . . + 3+2+1$
The second line is just a repeat of the first but with the terms in reverse order.
Then adding the two lines the right hand side becomes $n$ lots of $n+1$
So $2T_n=n(n+1)$ and since everything was added in twice,
$T_n=\frac{n(n+1)}{2}$.
David from Sha Tin College used a known general result for any progression that steps up by a fixed amount term on term
$\frac{n}{2}(2a+(n-1)d)$
where n is the number of terms, a is the starting term and d is that step up.
If the step up is equal to 1, and the start value is also 1, you can see that this is the same result as Curt demonstrated.
Continuing with the Pentagonal numbers
The diagram shows $P_4=3T_3+4$
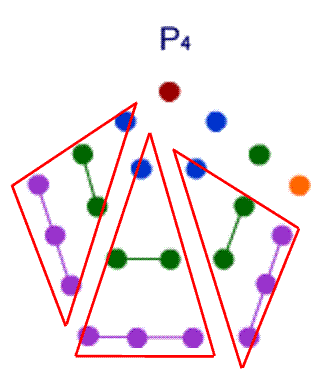
And in general $P_n=3T_{n-1}+n$
Now using the result for $T_n$ to see $P_n$ in terms of $n$
$P_n=\frac{3n(n-1)}{2}+n$
We now have to show that three times that result is a triangle number
$3P_n=3[\frac{3n(n-1)+2n}{2}]$ and is the same as $3[\frac{3n^2-n}{2}]$
or
$\frac{3n(3n-1)}{2}$
And that's the same as $T_{3n-1}$ the required result.
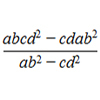

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Triangles Within Pentagons
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Curt from Reigate College started by getting a general formula for Triangle numbers
$T_n = 1 + 2 + 3+ . . . +(n-1) + n$
$T_n = n + (n-1) + . . . + 3+2+1$
The second line is just a repeat of the first but with the terms in reverse order.
Then adding the two lines the right hand side becomes $n$ lots of $n+1$
So $2T_n=n(n+1)$ and since everything was added in twice,
$T_n=\frac{n(n+1)}{2}$.
David from Sha Tin College used a known general result for any progression that steps up by a fixed amount term on term
$\frac{n}{2}(2a+(n-1)d)$
where n is the number of terms, a is the starting term and d is that step up.
If the step up is equal to 1, and the start value is also 1, you can see that this is the same result as Curt demonstrated.
Continuing with the Pentagonal numbers
The diagram shows $P_4=3T_3+4$
And in general $P_n=3T_{n-1}+n$
Now using the result for $T_n$ to see $P_n$ in terms of $n$
$P_n=\frac{3n(n-1)}{2}+n$
We now have to show that three times that result is a triangle number
$3P_n=3[\frac{3n(n-1)+2n}{2}]$ and is the same as $3[\frac{3n^2-n}{2}]$
or
$\frac{3n(3n-1)}{2}$
And that's the same as $T_{3n-1}$ the required result.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.

