Skip over navigation
To find the formula for this combinaton of three reflections requires very little knowledge of complex numbers. All you have to do is to combine the complex maps as you combine functions.. The example shows the power of complex numbers as a tool for working with transformations in the plane.
In the problem Complex Rotations you see another examle of using complex numbers for work with transformations.
The problems Rots and Refs and Reflect Again are examples of the use of matrices for work with transformations.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Footprints
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Teachers' Resources
To find the formula for this combinaton of three reflections requires very little knowledge of complex numbers. All you have to do is to combine the complex maps as you combine functions.. The example shows the power of complex numbers as a tool for working with transformations in the plane.
In the problem Complex Rotations you see another examle of using complex numbers for work with transformations.
The problems Rots and Refs and Reflect Again are examples of the use of matrices for work with transformations.
This problem is about combinations of reflections. The problem Reflect Again uses matrices to show that the combination of two reflections in intersecting mirror lines gives a rotation.
You may also like
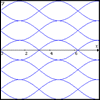
Sine Problem
In this 'mesh' of sine graphs, one of the graphs is the graph of the sine function. Find the equations of the other graphs to reproduce the pattern.
The Use of Mathematics in Computer Games
An account of how mathematics is used in computer games including geometry, vectors, transformations, 3D graphics, graph theory and simulations.

