Skip over navigation
Well done Rhema from Crown Woods School, Simon from Elizabeth College, Guernsey,Trevor from Queen Elizabeth's School, Barnet and Andrei from Tudor Vianu National College, Bucharest, Romania, you all sent in good solutions. To find the solution as a numerical approximation, Andrei used interval halving and a graphical method, Trevor and Simon used the Newton-Raphson method, Trevor used a spreadsheet for the calculations and Simon wrote a program in C to do the calculations.
Case (i)
If $a = b$ the equation $a^x + b^x = 1$ where $0< a, b < 1$ and $a + b < 1$ becomes $2a^x =1 $. Then $\log 2 + x \log a = 0$ so the solution can be given in three equivalent forms: $$x = {-\log 2 \over \log a} = {\log 0.5 \over \log a } = {\log 2 \over \log 1/a}.$$ Note we can use natural logarithms here or logarithms to any base.
Case (ii)
Solve $a^x + b^x = 1$, where $a=1/2$ and $b=1/4$. The equation is: $$(1/2)^x + (1/4)^x = 1,$$ Here you could substitute $y = (1/2)^x$ but Trevor multiplied by $4^x$ and used the substitution $y = 2^x$. By Trevor's method: $$4^x/2^x + 1 = 4^x$$ So $$2^x + 1 = (2^x)^2.$$ and the equation becomes: $y + 1= y^2$ or $y^2- y- 1 = 0$. Using the quadratic formula, the negative solution to the quadratic can be ignored as $2^x$ is never negative, so the solution is: $$y={1+ \sqrt 5 \over 2}$$ (note this equals the golden ratio, $\phi $). Therefore $2^x = \phi$ and so $x\ln 2 = \ln \phi$ and the solution is: $$x= {\ln \phi \over \ln 2} ={ \ln (1 + \sqrt 5)/2 \over \ln 2}$$ giving $x = 0.69424$ to 5 significant figures
Case (iii)
This is Andrei's method using interval halving:
Here I observe that I cannot solve the equation directly. First I shall prove that for any $0 < a, b < 1$, with $a + b < 1$, the equation $a^x + b^x = 1$ has a unique solution. Let $f: [0,1] \to R, f(x) = a^x + b^x - 1$ then $$f(0) = 1 > 0, f(1) = a + b - 1 < 0$$ and $f$ is a continuous function, so $f(x) = 0$ has at least one solution in its interval of definition. I shall now prove it is unique. The derivative $$f'(x) = a^x \ln a + b^x \ln b < 0,$$ as $a$ and $b < 1$. So, $f$ is strictly decreasing and the solution is unique.
For the case of the problem, $a =1/2$ and $b = 1/3$ I cannot find the exact value of the root, but I can find a good approximation of the solution. I shall use the interval halving method. Let $x_0$ be the root. The first value that I choose is 1/2.
Here is Trevor's spreadsheet for this calculation.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Equation Attack
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done Rhema from Crown Woods School, Simon from Elizabeth College, Guernsey,Trevor from Queen Elizabeth's School, Barnet and Andrei from Tudor Vianu National College, Bucharest, Romania, you all sent in good solutions. To find the solution as a numerical approximation, Andrei used interval halving and a graphical method, Trevor and Simon used the Newton-Raphson method, Trevor used a spreadsheet for the calculations and Simon wrote a program in C to do the calculations.
Case (i)
If $a = b$ the equation $a^x + b^x = 1$ where $0< a, b < 1$ and $a + b < 1$ becomes $2a^x =1 $. Then $\log 2 + x \log a = 0$ so the solution can be given in three equivalent forms: $$x = {-\log 2 \over \log a} = {\log 0.5 \over \log a } = {\log 2 \over \log 1/a}.$$ Note we can use natural logarithms here or logarithms to any base.
Case (ii)
Solve $a^x + b^x = 1$, where $a=1/2$ and $b=1/4$. The equation is: $$(1/2)^x + (1/4)^x = 1,$$ Here you could substitute $y = (1/2)^x$ but Trevor multiplied by $4^x$ and used the substitution $y = 2^x$. By Trevor's method: $$4^x/2^x + 1 = 4^x$$ So $$2^x + 1 = (2^x)^2.$$ and the equation becomes: $y + 1= y^2$ or $y^2- y- 1 = 0$. Using the quadratic formula, the negative solution to the quadratic can be ignored as $2^x$ is never negative, so the solution is: $$y={1+ \sqrt 5 \over 2}$$ (note this equals the golden ratio, $\phi $). Therefore $2^x = \phi$ and so $x\ln 2 = \ln \phi$ and the solution is: $$x= {\ln \phi \over \ln 2} ={ \ln (1 + \sqrt 5)/2 \over \ln 2}$$ giving $x = 0.69424$ to 5 significant figures
Case (iii)
This is Andrei's method using interval halving:
Here I observe that I cannot solve the equation directly. First I shall prove that for any $0 < a, b < 1$, with $a + b < 1$, the equation $a^x + b^x = 1$ has a unique solution. Let $f: [0,1] \to R, f(x) = a^x + b^x - 1$ then $$f(0) = 1 > 0, f(1) = a + b - 1 < 0$$ and $f$ is a continuous function, so $f(x) = 0$ has at least one solution in its interval of definition. I shall now prove it is unique. The derivative $$f'(x) = a^x \ln a + b^x \ln b < 0,$$ as $a$ and $b < 1$. So, $f$ is strictly decreasing and the solution is unique.
For the case of the problem, $a =1/2$ and $b = 1/3$ I cannot find the exact value of the root, but I can find a good approximation of the solution. I shall use the interval halving method. Let $x_0$ be the root. The first value that I choose is 1/2.
\begin{eqnarray} f(1/2) = 0.28 > 0 \Rightarrow
1/2 < x_0 < 1 & : & f(3/4) = 0.03 > 0\Rightarrow
3/4 < x_0 < 1 \\ f(7/8) = -0.07 < 0 \Rightarrow 3/4 <
x_0 < 7/8 & : & f(13/16) = -0.02 < 0 \Rightarrow 3/4
< x_0 < 13/16 \\ f(25/32) = 0.005 > 0 \Rightarrow 25/32
< x_0 < 13/16 & : & f(51/64) = - 0.007 < 0
\Rightarrow 25/32 < x_0 < 51/64\\ f(101/128) = -0.001 < 0
\Rightarrow 25/32 < x_0 < 101/128 & : & f(201/256) =
0.002 > 0 \Rightarrow 201/256 < x_0 < 101/128 \\
f(403/512) = 0.0006 > 0 \Rightarrow 403/512 < x_0 <
101/128 & : & f(707/1024) = -0.0001 < 0 \Rightarrow
403/512 < x_0 < 807/1024.\\ \end{eqnarray}
So, $0.7871 < x_0 < 0.7880$. Continuing the procedure, I
could find a better approximation for the root $x_0$. 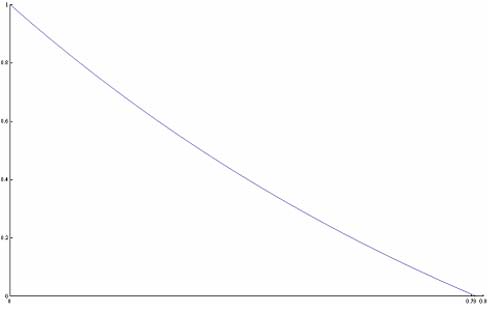 |
Another method, though less precise, would have been a graphical one. In this graph I have plotted f(x) and the solution is given by the intersection with the x-axis. |
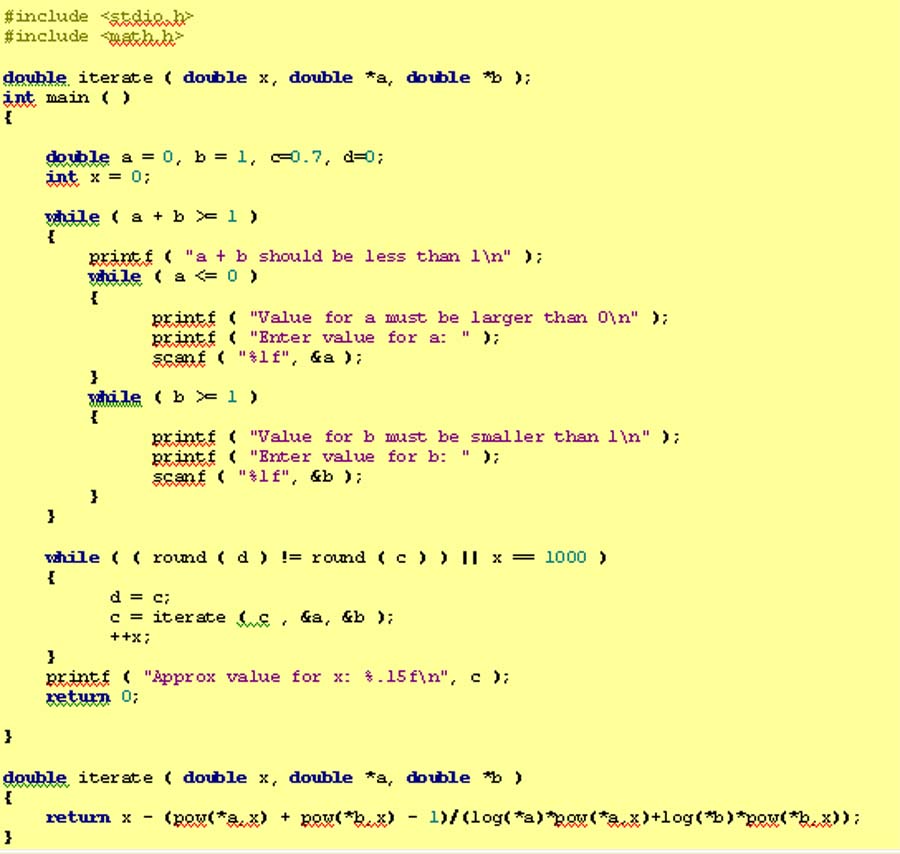
Simon used the Newton-Raphson method
and a computer to work out the answers to this part
Differentiating the function $f(x) = a^x + b^x - 1$ gives
$f'(x)=\ln a . a^x + \ln b . b^x.$ Using the Newton-Raphson
formula: $$x_{r+1} = x_r - {f(x_r)\over f'(x_r)}$$ gives $$x_{r+1}
= x_r - {a^{x_r} + b^{x_r} - 1 \over \ln a . a^{x_r} + \ln b .
b^{x_r}}.$$ As the notes allow us to use a programmable calculator,
which I interpreted to mean computer, as that is essentially what a
computer is, I coded a script in C to do this problem for me.
The approximate value for x: 0.784453067133075 (using $a=1/2,
\ b=1/3$.)

Here is Trevor's spreadsheet for this calculation.
You may also like
Big, Bigger, Biggest
Which is the biggest and which the smallest of $2000^{2002}, 2001^{2001} \text{and } 2002^{2000}$?
Infinite Continued Fractions
In this article we are going to look at infinite continued fractions - continued fractions that do not terminate.
Gosh Cosh
Explore the hyperbolic functions sinh and cosh using what you know about the exponential function.

