Skip over navigation
This is a difficult visualisation problem to tackle, not least because is it very difficult to create a physical model with which it is possible to experiment with the slicing. Visualisation is thus crucially required.
The problem can be attempted at various levels, from having an educated guess at the answer to providing a proof of the maximum possible number of pieces.
If solvers are unable to prove the maximum number of pieces they should certainly be encouraged to describe their best effort at a slicing as clearly and convincingly as possible. Try to establish the existence of an upper bound on the number of pieces.
In practice, the solver may be able to spot the answer quite quickly, but providing an explanation of the answer may be very hard. Solvers should be encouraged to try to explain their answer as clearly as possible in words if a sound mathematical argument cannot intially be provided.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cheese Cutting
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This is a difficult visualisation problem to tackle, not least because is it very difficult to create a physical model with which it is possible to experiment with the slicing. Visualisation is thus crucially required.
The problem can be attempted at various levels, from having an educated guess at the answer to providing a proof of the maximum possible number of pieces.
If solvers are unable to prove the maximum number of pieces they should certainly be encouraged to describe their best effort at a slicing as clearly and convincingly as possible. Try to establish the existence of an upper bound on the number of pieces.
In practice, the solver may be able to spot the answer quite quickly, but providing an explanation of the answer may be very hard. Solvers should be encouraged to try to explain their answer as clearly as possible in words if a sound mathematical argument cannot intially be provided.
You may also like
Circles Ad Infinitum
A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
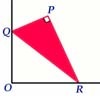
Set Square
A triangle PQR, right angled at P, slides on a horizontal floor with Q and R in contact with perpendicular walls. What is the locus of P?
Wrapping Gifts
A box of size a cm by b cm by c cm is to be wrapped with a square piece of wrapping paper. Without cutting the paper what is the smallest square this can be?

