Skip over navigation
Answer: 9 different remainders (0, 1, 2, 3, 4, 5, 6, 7, 16)
Remainder is 16 for the larger numbers tested
Had to multiply by $n-4$ for the larger values of $n$, try this algebraically: $(n-4)(n+4)=n^2-16$
So $n^2 = \underbrace{(n-4)(n+4)}_{\text{multiple of }n+4} + 16$
So the remainder is the same as the remainder when $16$ is divided by $n+4$
This will be $16$ if $n+4\gt16$ so if $n\gt12$.
Check values for $n=8$ to $n=12$ ($n$ up to $7$ shown above)
So possible remainders are 0 - 7 and 16, 9 possibilites.
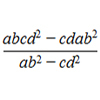

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Leftovers
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 9 different remainders (0, 1, 2, 3, 4, 5, 6, 7, 16)
| $n$ | $n^2$ | $n+4$ | remainder |
|---|---|---|---|
| 1 | 1 | 5 | 1 |
| 2 | 4 | 6 | 4 |
| 3 | 9 | 7 | 2 |
| 4 | 16 | 8 | 0 |
| 5 | 25 | 9 | 7 |
| 6 | 36 | 10 | 6 |
| 7 | 49 | 11 | 5 |
| ... | ... | ||
| Not much pattern so far | |||
| ... | ... | ||
| 20 | 400 | 24 | 24$\times$15 = 240 + 120 = 360 24$\times$16 = 360 + 24 = 384 remainder is 16 |
| 100 | 10000 | 104 | 104$\times$100 = 10400 104$\times$96 = 10400 - 4016 = 10000 - 16 remainder is 16 |
| 101 | 10201 | 105 | 105$\times$100 = 10500 105$\times$97 = 10500 - 315 = 10200 - 16 remainder is 16 |
Remainder is 16 for the larger numbers tested
Had to multiply by $n-4$ for the larger values of $n$, try this algebraically: $(n-4)(n+4)=n^2-16$
So $n^2 = \underbrace{(n-4)(n+4)}_{\text{multiple of }n+4} + 16$
So the remainder is the same as the remainder when $16$ is divided by $n+4$
This will be $16$ if $n+4\gt16$ so if $n\gt12$.
Check values for $n=8$ to $n=12$ ($n$ up to $7$ shown above)
| $n$ | $n+4$ | remainder when $16$ divided by $n+4$ |
|---|---|---|
| 8 | 12 | 4 |
| 9 | 13 | 3 |
| 10 | 14 | 2 |
| 11 | 15 | 1 |
| 12 | 16 | 0 |
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.

