Skip over navigation
Here's a spreadsheet file that helps - Peaches Generally
There are three pages or sheets in this file (look for the coloured tabs at the bottom)
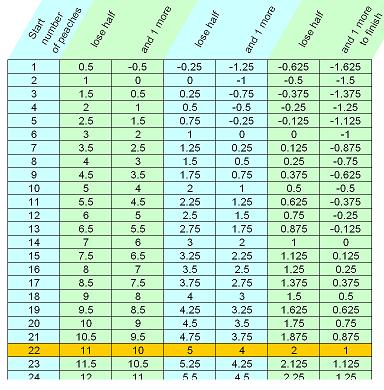
The first called 'Forwards' shows the basic Peaches problem and the solution of 22 is picked out in yellow.
 The third sheet is called 'with Variables' and will help you
generalize.
The third sheet is called 'with Variables' and will help you
generalize.
The general process is to have repetitions of two alternating actions. One action is to multiply by a constant amount. In the basic Peaches problem, that multiplier is 0.5, when half the peaches remain. The second action is to add, or subtract, a constant amount. That value is -1 in the original setup.
Experiment varying these two values. You should quickly find some patterns to think about.
You may also notice that there isn't really a 'forwards' or 'backwards', just a line of values and a repeated pair of actions which takes you along the line in the direction you choose. Choosing the opposite direction just uses the inverses of those actions and in the opposite order.
There's a multiplier, involving the interest rate, and a constant addition, the amount of the loan paid off each month.
That addition is negative because the loan amount, which is the quantity we really care about, is reduced rather tha increased by each monthly payment.
And if you do get that far you'll have seen something very important about mathematics. A monkey eating peaches might seem a rather childish puzzle, but once we start to generalize the problem we find a valuable abstract form which will appear in the most surprising places.
A mathematician's task is to have a good stock of these abstract forms and to know their key properties.
Mathematicians are always looking for new forms and new properties; posing questions around simple situations is a great way to make these discoveries.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Peaches in General
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here's a spreadsheet file that helps - Peaches Generally
There are three pages or sheets in this file (look for the coloured tabs at the bottom)
The first called 'Forwards' shows the basic Peaches problem and the solution of 22 is picked out in yellow.
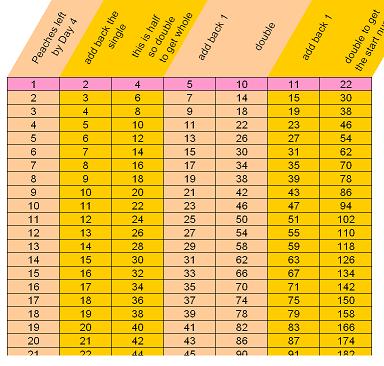
The second sheet is called 'Backwards' which starts with the
end number of peaches and works back to the start number.
This is more efficient. Can you see why ?
The general process is to have repetitions of two alternating actions. One action is to multiply by a constant amount. In the basic Peaches problem, that multiplier is 0.5, when half the peaches remain. The second action is to add, or subtract, a constant amount. That value is -1 in the original setup.
Experiment varying these two values. You should quickly find some patterns to think about.
What's going on, and why does it happen ?
You may also notice that there isn't really a 'forwards' or 'backwards', just a line of values and a repeated pair of actions which takes you along the line in the direction you choose. Choosing the opposite direction just uses the inverses of those actions and in the opposite order.
Once you have a really good feel for this you might like to find out about Repayment Mortgages.
There's a multiplier, involving the interest rate, and a constant addition, the amount of the loan paid off each month.
That addition is negative because the loan amount, which is the quantity we really care about, is reduced rather tha increased by each monthly payment.
And if you do get that far you'll have seen something very important about mathematics. A monkey eating peaches might seem a rather childish puzzle, but once we start to generalize the problem we find a valuable abstract form which will appear in the most surprising places.
A mathematician's task is to have a good stock of these abstract forms and to know their key properties.
Mathematicians are always looking for new forms and new properties; posing questions around simple situations is a great way to make these discoveries.
You may also like
Euler's Squares
Euler found four whole numbers such that the sum of any two of the numbers is a perfect square...
Odd Differences
The diagram illustrates the formula: 1 + 3 + 5 + ... + (2n - 1) = n² Use the diagram to show that any odd number is the difference of two squares.
Tree Tops
Can you make sense of information about trees in order to maximise the profits of a forestry company?

