Skip over navigation
James Bell from the MacMillan academy was the first person to crack this toughnut, with this solution. He also noted that the problem as it stood only held for positive random variables -- well spotted. Well dones James!
For the first part James cleverly used random variables which only took a single value to work out that $??$ must equal $1$:
Part 1:
Consider $X$ such that $P(X=10)=1$ $E(|X|)=10$ taking $a=9$ we get left hand side equal to $1$ so the right handside must equal at least $1 =\frac{10}{9^{??}}$. If $??$ were $2$ or greater this wouldn't be satisfied.
Now consider $P(X=0.5)=1$ so $E(|X|)=0.5$. Taking $a=0.45$ we get left hand side equal to $1$ so the right handside must equal at least $1 =\frac{0.5}{0.45^{??}}$. If $??$ were $0$ or less this wouldn't be satisfied and so $??=1$.
Part 2:
Our task is to design a distribution such that the chance of $X$ being at least $2\sigma$ from the mean is maximised.
James first argues that a distribution which satisfied the inquality exactly must have a maximum value of $2\sigma$ by shifting probability around. Some more details would be needed for a fully convincing explanation, but the argument is in essence correct and shows very sophisticated statistical reasoning .
If a solution existed where $X$ could take a value greater than $2\sigma$ from the mean then we could use this to create a new distribution $Y$ by changing the values of events leading to a difference being greater than $2\sigma$ to values leading to a difference of $2\sigma$, thus making the probability of the difference being greater than $2\sigma$ zero. Of course, this would decrease $2\sigma$ for $Y$; some of the probability for $Y$ could be moved from near the mean to outside $2\sigma$ for $Y$ without moving $2\sigma$ for $Y$ as far out to where it was originally for $X$, meaning that the probability of $|Y-\mu|$ being greater than $2\sigma$ would increase above $\frac{1}{4}$. As we know this to be impossible, any such distribution must have $P(|X-\mu|> 2\sigma)=0$.
With this insight, James was able to search for a solution
Assuming symmetry, to find a solution let us set
$$
P(X-\mu=2\sigma)=P(\mu-X=2\sigma)=0.125\,,
$$
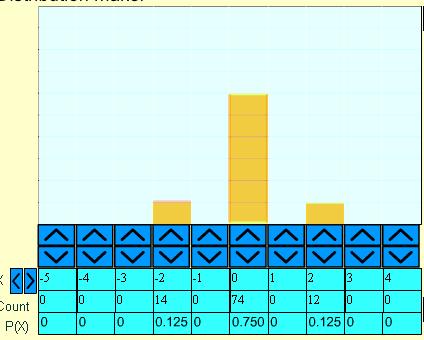
as together they must add to $0.25$ or $\frac{1}{4}$ the other $\frac{3}{4}$ must be distributed right on the mean in order to makle the variance as small as possible which suggests the distribution attached for $\sigma=1\,, \mu=0$, and sure enough calculating sigma from the distribution gives $\sigma=1$ as well confirming that it works.
Here is the picture:
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Random Inequalities
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
James Bell from the MacMillan academy was the first person to crack this toughnut, with this solution. He also noted that the problem as it stood only held for positive random variables -- well spotted. Well dones James!
For the first part James cleverly used random variables which only took a single value to work out that $??$ must equal $1$:
Part 1:
Consider $X$ such that $P(X=10)=1$ $E(|X|)=10$ taking $a=9$ we get left hand side equal to $1$ so the right handside must equal at least $1 =\frac{10}{9^{??}}$. If $??$ were $2$ or greater this wouldn't be satisfied.
Now consider $P(X=0.5)=1$ so $E(|X|)=0.5$. Taking $a=0.45$ we get left hand side equal to $1$ so the right handside must equal at least $1 =\frac{0.5}{0.45^{??}}$. If $??$ were $0$ or less this wouldn't be satisfied and so $??=1$.
Part 2:
Our task is to design a distribution such that the chance of $X$ being at least $2\sigma$ from the mean is maximised.
James first argues that a distribution which satisfied the inquality exactly must have a maximum value of $2\sigma$ by shifting probability around. Some more details would be needed for a fully convincing explanation, but the argument is in essence correct and shows very sophisticated statistical reasoning .
If a solution existed where $X$ could take a value greater than $2\sigma$ from the mean then we could use this to create a new distribution $Y$ by changing the values of events leading to a difference being greater than $2\sigma$ to values leading to a difference of $2\sigma$, thus making the probability of the difference being greater than $2\sigma$ zero. Of course, this would decrease $2\sigma$ for $Y$; some of the probability for $Y$ could be moved from near the mean to outside $2\sigma$ for $Y$ without moving $2\sigma$ for $Y$ as far out to where it was originally for $X$, meaning that the probability of $|Y-\mu|$ being greater than $2\sigma$ would increase above $\frac{1}{4}$. As we know this to be impossible, any such distribution must have $P(|X-\mu|> 2\sigma)=0$.
With this insight, James was able to search for a solution
Assuming symmetry, to find a solution let us set
$$
P(X-\mu=2\sigma)=P(\mu-X=2\sigma)=0.125\,,
$$
as together they must add to $0.25$ or $\frac{1}{4}$ the other $\frac{3}{4}$ must be distributed right on the mean in order to makle the variance as small as possible which suggests the distribution attached for $\sigma=1\,, \mu=0$, and sure enough calculating sigma from the distribution gives $\sigma=1$ as well confirming that it works.
Here is the picture:

You may also like
Into the Exponential Distribution
Get into the exponential distribution through an exploration of its pdf.

