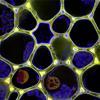
Packing 3D Shapes

Why do this problem ?

This problem will allow students to engage with visualisations of 3D shapes. By exploring the shapes present in nature, students will begin to develop their skills of geometrical reasoning in a concrete setting.

Possible approach

This question could be posed individually or for group discussion. This problem also works effectively when students are given time to reflect on the question and look for packings in nature. Ask the question and let students consider it over, say, a week. What shapes and packings have they noticed in nature? Could they find any images to share? Then consider the questions of efficient packings. This results might make an effective display.

Key questions

• Can you clearly describe the underlying mathematical shapes in words?
• Can you describe your method of packing the shapes clearly in words? Can you draw an effective diagram?
• How many different sensible packing methods might you try for different shapes?

Possible extension

Can you consider the efficiency of the various packings? (i.e. roughly what percentage of space is taken up by the packed shapes)

Possible support