Skip over navigation
On a weekend break a short while ago I saw this market cross.
On the side perhaps you can see that it has a plaque with distances to local and more distant towns:
Where was I?
What is the minimum amount of information you need to know where I was? Is some of the information redundant?
Is some of the information more useful than other parts?
How accurate can you be about exactly where I was from the distances that are given?
What can you find out about this place?
Can you make up similar problems of your own?
Where Am I?
Age 11 to 16
Challenge Level 
On a weekend break a short while ago I saw this market cross.
On the side perhaps you can see that it has a plaque with distances to local and more distant towns:
Where was I?
What is the minimum amount of information you need to know where I was? Is some of the information redundant?
Is some of the information more useful than other parts?
How accurate can you be about exactly where I was from the distances that are given?
Then why not think about the following questions:
Why has someone bothered to include so much information?What can you find out about this place?
Can you make up similar problems of your own?
You may also like
Just Rolling Round
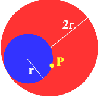
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?
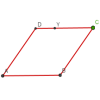
Roaming Rhombus
We have four rods of equal lengths hinged at their endpoints to form a rhombus ABCD. Keeping AB fixed we allow CD to take all possible positions in the plane. What is the locus (or path) of the point D?