Skip over navigation
Where Am I?
Age 11 to 16
Challenge Level 
Why do this problem?
This problem encourages students to apply simple loci and the use of scales to a real context. It can be used to focus on identification of necessary and redundant information, accuracy and methods of measurement and representing information. There is also a great opportunity to work with the Geography department.Possible approach
You might wish to start with an activity similar to that
described in "Possible Support" below. If you do this you might use
some string to emphasise the locus of points that are a given
distance from a fixed point.
What about all the places in the school that are 100m from
your classroom? Would you measure direct distances (as the crow
flies) or the distance you would actually walk. So, for example,
the edge of the playground may be 50m from the clasroom window but
it is a 100m walk because you would need to leave by the classroom
door and along the corridors to the door into the playground.
This activity can be used with paper-based maps or map
software that is available free on the internet. The advantage of
paper is the opportunity it offers for drawingcircles to represent
the loci. Ask pupils to use transparencies to draw their circles so
that maps can be reused. They will also need string or thread if
they are to measure distances along the roads rather than "as the
crow flies".
Show the class the problem and leave them working in pairs or
small groups to try to find the location.
Share ideas in larger groups - ask them to discuss the other
questions posed.
Ask groups to prepare posters of their findings to dispaly on the
board,or create their own examples of similar problems based on a
local, national or international scale. They shoulddicuss levels of
accuracy as the scale at which they work increases or
decreases.Key questions
Is there redundant information?
How accurate can we be?
What limits the accuracy?
Why do the distances on the sign differ from those we can
calculate from a modern map, routeplanning software of Google
Earth?
Possible extension
Students create problems of their own. Use local geography or even the school buildings themselves to pose similar problems. Why not use these as the basis of a bank of problems for other students to try?Possible support
Start with a practical activity in the playground:
Can you all stand so that you are 6 metres from Amy?
Can you all stand so that you are 6 metres from Amy and 10
metres from Ben?
Who is within 7 metres of Asha and how could we check?
And so on...
Then use some simple maps to locate places a fixed distance
from the school or familiar landmark before moving on to the
problem or something similar but based in a more familiar setting
such as the school itself.
You may also like
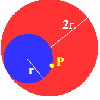
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?
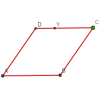
Roaming Rhombus
We have four rods of equal lengths hinged at their endpoints to form a rhombus ABCD. Keeping AB fixed we allow CD to take all possible positions in the plane. What is the locus (or path) of the point D?