Skip over navigation
In a public building in England, I found this wonderful tiled floor:
Really interesting I thought, because so much that looked the same at first glance was in fact different.
Look at the three images of the patterns I found along the centre of the tiling (below).
What is the same about them and what is different?
Now look again at the picture of the whole of the main tiled area. It was made from nine complete patterns each like one of the three above.
At the ends there were partial patterns, both like the one in the foreground. The pattern was surrounded by a rectangle of black tiles with some further tiling beyond.
Describe the pattern.
How many of each type of tile are included in the pattern?
How could you check?
Can you reproduce parts of the pattern?
Can you extend it sideways?
Have a set of about a dozen of each of the basic tiles for learners to recreate each pattern to start with.
Tiles in a Public Building
Age 7 to 11
Challenge Level 
Tiles in a Public Building
In a public building in England, I found this wonderful tiled floor:
Really interesting I thought, because so much that looked the same at first glance was in fact different.
Look at the three images of the patterns I found along the centre of the tiling (below).
What is the same about them and what is different?
Now look again at the picture of the whole of the main tiled area. It was made from nine complete patterns each like one of the three above.
At the ends there were partial patterns, both like the one in the foreground. The pattern was surrounded by a rectangle of black tiles with some further tiling beyond.
Describe the pattern.
How many of each type of tile are included in the pattern?
How could you check?
Can you reproduce parts of the pattern?
Can you extend it sideways?
Why do this problem?
This problem demonstrates a practical application of symmetry and tessellations. It offers opportunities not only to investigate and analyse the images but to create similar patterns using the same basic ideas.
Possible approach
This document contains the four images which can be copied onto cards for use by groups of learners. First spend some time investigating the basic units for the floor tiling and how they are combined (for example, six different square tiles all linked into cross patterns using the brown and black spacers).
Start by looking at images 2 and 3. What is the same and what is different about them?
Now compare these with image 1. How does this image differ and how is it the same?
Now pose the main problem and ask learners to calculate the numbers of each tile they would need to create the pattern.
At this point learners could create their own tile patterns (groups produce one pattern each), which are copied onto coloured paper. The class could then work collaboratively, using combinations of these tiles to produce a display for a "tiled floor".
Key questions
How is the symmetry of each basic pattern the same and how are they different?
How could you extend the pattern to the sides? Is anything implied by the edges that are visible?
Possible extension
Extend the idea to tessellating a set of different tiles. You might like to use ATM MATs .
Possible support
Have a set of about a dozen of each of the basic tiles for learners to recreate each pattern to start with.You may also like
Clock Hands
This investigation explores using different shapes as the hands of the clock. What things occur as the the hands move.
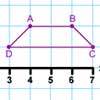
Transformation Tease
What are the coordinates of this shape after it has been transformed in the ways described? Compare these with the original coordinates. What do you notice about the numbers?
Penta Play
A shape and space game for 2, 3 or 4 players. Be the last person to be able to place a pentomino piece on the playing board.