Skip over navigation
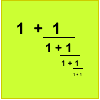
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Genes of Gilgamesh
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This is an interesting, quick question for use whilst studying
genetics and will draw the learners in to the mathematical issues
surround inheritance and fractions.
Possible approach
Discuss the question before attempting a detailed solution.
Some students might see it as possible to make (GGM), others might
see it as impossible. The challenge will be in explaining clearly
why this is or is not the case. Do not allow students to get away
with saying 'it is obvious' one way or the other. A full
explanation will require clear reasoning, and this should be
encouraged. Help by asking 'why is it obvious?' Part of the
subtlety will be that the parents, grandparents and other
generations could be made from a variety of mixes of (GM). Students
will need to be clear that they have considered this point.
Key questions
- Do you think that it is possible to make (GGM)?
- What other ratios (e.g. GGGGMM) would be equivalent to (GGM)?
- What possible fractions would be within 1% of (GGM)?
Possible extension
- Generally speaking, starting from a stock of pure G and pure M, can you determine thestock of all possible descendants?
- Can students invent a similar question of their own?
Possible support
Students struggling to get started could be asked directly to
work out possible great-grandparents for (GM), (GGGM),
(GGGGGGGM)
You may also like
There's a Limit
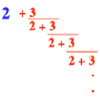
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?
Not Continued Fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers?

