Skip over navigation
Building up Friction
Age 16 to 18
Challenge Level 
This problem consists of a sequence of ideas concerning the configuration of hoop and pole as shown in the diagram below.
 |
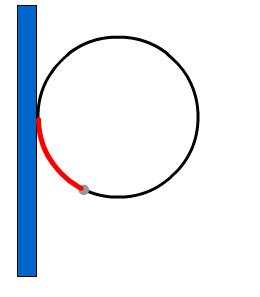A rigid hoop of radius $r$ is attached to a vertical pole. A light ideal spring of unstretched length $L$ and spring constant $k$ is attached at one end at the point of contact of the hoop to the pole. A bead of mass $m$ is attached to the other end of the spring and the bead and spring are threaded onto the hoop, so they can slide around its circumference. |
If the hoop configuration is frictionless, what will be the possible range of positions of the bead for a stationary configuration?
What constants in the problem will affect the locations of these stationary positions? In particular, will they depend on the values of $r$ and $L$? Test your intuition by finding these values.
How will these results change if there is a coefficient of friction $\mu$ between the bead and the hoop? (The spring sliding around the hoop remains frictionless).
Can values of the constants be found so that the bead can remain stationary at any point on the hoop? Back up your conjecture with a mathematical analysis.
Imagine that the bead is stretched to a certain position and released. How many qualitatively different types of motion might result?
You may also like
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?
Stonehenge
Explain why, when moving heavy objects on rollers, the object moves twice as fast as the rollers. Try a similar experiment yourself.
Maximum Flow
Given the graph of a supply network and the maximum capacity for flow in each section find the maximum flow across the network.