Whose Line Graph Is it Anyway?

Age 16 to 18

Challenge Level Yellow star

Scientific processes involving two variables can often be represented using equations and line graphs.

In this problem, $9$ processes, their equations and graphs have been mixed up and shown below. In each case, the two variables are represented by the letters $x$ and $y$ and the labels from the axes of the graphs have been removed.

Which can you match up? What is the interpretation of the variables $x$ and $y$ in each case?

Can you identify the physical interpretation of three key points on each of the graphs?

Processes

Number of rapidly dividing bacteria present in a food-limited environment, starting from a small initial sample.
Concentration in the blood of a drug following an injection.
Angle of oscillation of a real pendulum of length $1$m in air.
Volume (litres) against pressure (atmospheres) for $1$ mole of an ideal gas at $0^\circ$ C.
Vertical distance travelled by a small, heavy ball dropped from a plane.
Rate of reaction of a catalysed reaction in terms of the concentration of reagent.
Number of rapidly dividing bacteria present in a food-rich environment, starting from a small initial sample.
Hours of daylight per day in a town in the far northern hemisphere.
Model of the distance of the Earth from the sun in astronomical units.

Line Graphs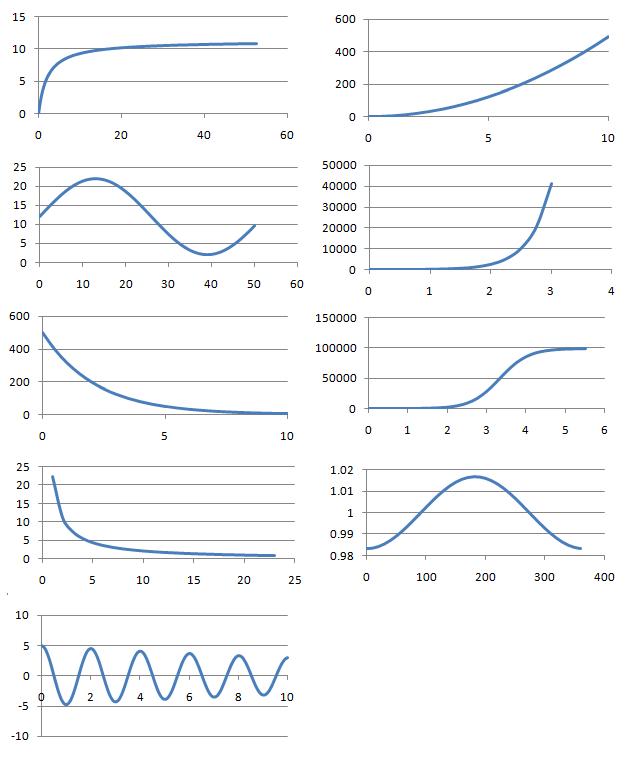
Equations

A: $y(x) = 4.9 x^2$

B: $y(x) =500 \times 2^{-0.6667x}$

C: $y(x) =1- 0.01671\cos(0.0172 x)$

D: $y(x) = 12+10\sin(0.121 x)$

E: $y(x) = 5\cos(3.13 x)e^{-0.05x}$

F: $y(x) = (11.3 x)/(2.1+x)$

G: $y(x) =10 \times 2^{4x}$

H: $y(x) = \frac{1000000}{10+(100000-10)2^{-4x}}$

I: $y(x)x = 22.4133$

The numbers have been carefully chosen to represent certain time/length/unit scales for particular physical phenomena. Can you deduce the reason for the choice of any of the numbers?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Whose Line Graph Is it Anyway?

You may also like

How Many Solutions?

Quartics

Power Up