Whose Line Graph Is it Anyway?

Age 16 to 18

Challenge Level Yellow star

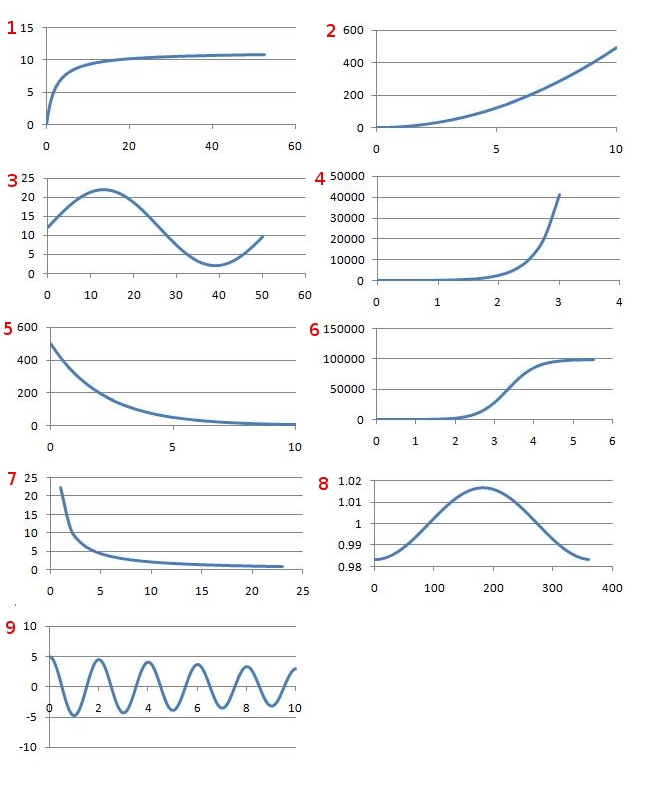
Process	Graph	Equation	Explanation
1	6	H	In a food-limited environment bacteria tend to maximum number after initial exponential growth (following lag phase)
2	5	B	Concentration will exponentially decay as drug is metabolised
3	9	E	Pendulum will have an sinusodial motion with a decaying amplitude due to damping from air resistance
4	7	I	Ideal gas equation $pV = nRT$ therefore pressure and volume are in a reciprocal relationship
5	2	A	Ball is small and heavy, therefore assume air resistance is negligible at first and so acceleration is constant. $s = ut + \frac{1}{2}at^2$ therefore for $u=0;\ a=g \Rightarrow s=\frac{1}{2}gt^2$ (qualitatively vertical speed represented by gradient of graph is increasing)
6	1	F	As concentration of reagent increases so does reaction rate, however as increase continues concentration of the catalyst becomes the limiting factor (saturation)
7	4	G	When not food limited, bacteria follow exponential growth after initial lag phase
8	3	D	Hours of daylight varies from a maximum at mid-summer to minimum at mid-winter, with a mean value of 12
9	8	C	Earth's orbit is not perfectly circular therefore small oscillations about mean distance (1 AU) with period of one year (note non-zero origin on vertical axis)

You may also like