Calculus Countdown

In the game of Calculus Countdown you are given the following four machines into which you insert cards with functions written on them; the four machines chew up the input card(s) and spit out new cards with functions written on them. You can put any output cards back into the machines if you like. The idea of the game is to hit certain target cards given a set of initial cards.
 
 

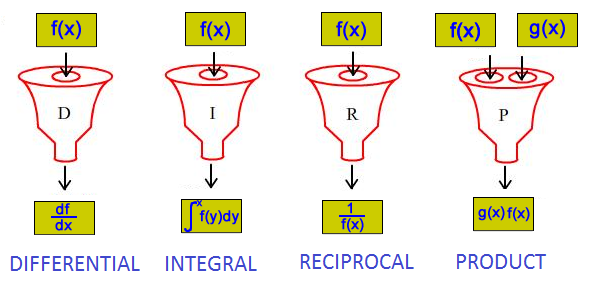
Let's play a game. You are given the following initial seven cards (no constants of integration from the integral machine and no repeats of cards, other than the pair of $e^x$s)
 
 
 
Which of the following targets could you hit starting with these cards? You can use a fresh set of seven cards for each new target.
 
 
 
Can you make a smaller set of cards which could hit each of these targets?
 
Why not invent your own set of starting cards and targets?