Skip over navigation
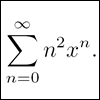

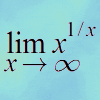
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Calculus Countdown
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem gives a great engaging context in which to practise calculus. It is very useful for getting across important ideas concerning integration and differentiation as operations, which will be useful at university in both science and maths courses.Possible approach
Initially play as a straightforward game to try to hit the
targets.
Students could then try to create new targets for their
friends to try to hit using the same initial functions.
You could then give the students the task of creating their
own game of Calculus Countdown.
Once students have hit a target they will need to communicate
their answers clearly. How might they write down an answer in a
clear and unambiguous way that can easily be interpreted by someone
else?
Key questions
What happens when you integrate or differentiate the starting
functions?
What would you have to integrate or differentiate in one step
to hit the targets? Does this help?
Possible extension
Interesting side questions which might emerge are: What
targets are possible? Can you prove that certain targets (such as
$\sqrt{x}$ or $3$) are impossible to hit? Clearly, proving the
impossibility of a target will require some clear thinking; be sure
that students concentrate on clearly writing down their
arguments.
Possible support
Focus on the first 3 targets.
You may also like
Generally Geometric
Generalise the sum of a GP by using derivatives to make the coefficients into powers of the natural numbers.
Bend
What is the longest stick that can be carried horizontally along a narrow corridor and around a right-angled bend?
Exponential Trend
Find all the turning points of y=x^{1/x} for x>0 and decide whether each is a maximum or minimum. Give a sketch of the graph.

