Beam Me Up

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

The curvature, $\kappa$, of a circle of radius $r$ (given by the equation $y=\sqrt{r^2-x^2}$) is defined to be $\frac{1}{r}$. The curvature of a more general curve $y=f(x)$ varies from point to point, and equals the curvature of the circle which just matches the 'bend' of the curve at that point. It has the formula

$$\kappa = \frac{y''}{(1+y'^2)^{\frac{3}{2}}}\;.$$

The angle $\psi$ by which a point on a curve has deviated from a straight line is $\psi = \int{\kappa}ds$. i.e. the angle deviated is the sum of the curvature up to that point. Think about this formula. Does it make sense? Just think about curvature for circles to begin with.



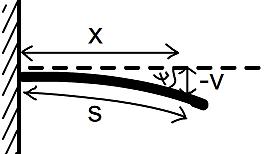
In structures, we generally expect the deflections of solid objects to be small. (Think of how little a bridge moves up and down when you walk on it, relative to its length.) So we can usually approximate the distance along a curved beam, $s$, as the linear distance, $x$, i.e. $\delta s \approx \delta x$.

Can you work out a formula for the vertical deflection (displacement) $v$ of a point on the curve, in terms of $\psi$ and $x$?

What about $v$ in terms of $\kappa$ and $x$?