Drawing Celtic Knots

Celtic knots are graphical representations of knots used for decoration by the ancient Celts. Here is a picture of an illuminated letter from a manuscript, showing intricate overlapping knots:

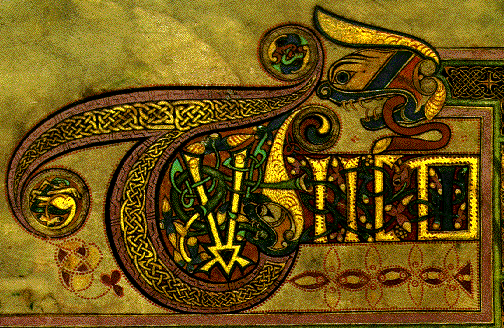
How about trying to draw some simple Celtic knots of your own? Watch the two videos, which show two different methods for drawing the same knot:

Alison's Video

Charlie's Video

Here are some images of completed knots. They have been coloured in so you can follow the different "ribbons" that make up the knot (click to enlarge):

You may find it useful to print off some of these grids (Word, pdf) to draw onto.

Alternatively, it is fairly simple to create your own grids by drawing faint diagonal lines on squared or square dotty paper. The straight lines needed to create the knots all go through the midpoints of the sides of the squares:

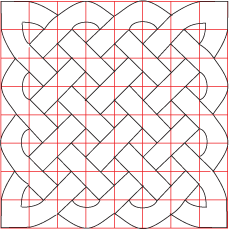
While you are drawing the Celtic knots, you may think of mathematical questions to ask.
Here are some questions that occured to us:

Try drawing some knots on square grids. What do you notice about the number of ribbons needed to create square knots? Can you explain your findings?

For rectangular knots, can you explain how the knot size determines the number of ribbons?

Is it possible to draw a rectangular Celtic knot without rotational symmetry?

Can you explain how the knot size determines the number of overlaps?

Send us your findings, and pictures of your knots.