Skip over navigation
In this case M = 5 and N = 3 so the number of ribbons is 1.
Therefore, if a square Celtic knot has side length x, the number of different ribbons will be x.
In this case x = 4 so the number of ribbons is 4.
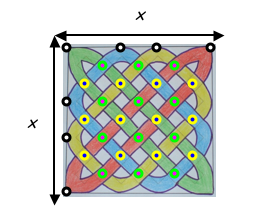
The number of crossovers for a square Celtic knot is $$2x^2 - 2x$$ or $$2x (x - 1)$$
Students from Garden International School also worked on this problem. Here is what Kenn, Jong Woong, Jayme and Marana sent us.
Drawing Celtic Knots
Age 11 to 14
Challenge Level 
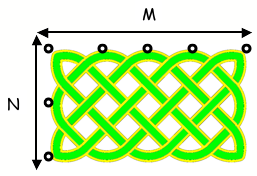
William from Barnton Community Primary School discovered that:
If there is a rectangular Celtic knot that is M by N then the
number of ribbons is the highest common factor of M and N.
In this case M = 5 and N = 3 so the number of ribbons is 1.
Therefore, if a square Celtic knot has side length x, the number of different ribbons will be x.
In this case x = 4 so the number of ribbons is 4.
The number of crossovers for a square Celtic knot is $$2x^2 - 2x$$ or $$2x (x - 1)$$
Students from Garden International School also worked on this problem. Here is what Kenn, Jong Woong, Jayme and Marana sent us.
Related Collections
You may also like
More on Mazes
There is a long tradition of creating mazes throughout history and across the world. This article gives details of mazes you can visit and those that you can tackle on paper.
Mathematical Patchwork
Jenny Murray describes the mathematical processes behind making patchwork in this article for students.
Turning the Place Over
As part of Liverpool08 European Capital of Culture there were a huge number of events and displays. One of the art installations was called "Turning the Place Over". Can you find our how it works?