Age 16 to 18

Article by Rosie Robison

Published 2010

Maths in the Undergraduate Physical Sciences

Are you planning to study engineering, physics or another course involving lots of applied mathematics at university?

In your first year you will undoubtedly take maths courses to bring you up to speed with many of the advanced mathematical techniques required in the serious applications of mathematics to the physical sciences.

Whilst courses and content do, of course, vary, there is a general core of content most physical scientists will encounter and make use of in their first year of study. Unfortunately, however, it is sometimes not immediately clear how the maths you are taught will be useful in the physical and practical applications.

This article lists some of the topics you are very likely to come across, and explains just some of the areas where they can be applied to physical science problems. The topics below also link to articles and problems where you can learn about them in more detail. The more familiar you are with these concepts and new vocabulary the smoother your transition to university should be. Good luck!

1. Vector manipulation

An important definition here is the cross product. This defines a vector ${\bf a} \times {\bf b}$ which is perpendicular to both ${\bf a}$ and ${\bf b}$, and has magnitude $\mid {\bf a} \mid \mid {\bf b} \mid \sin \theta$ . Suppose we have a spherical object which rotates about a fixed axis at a constant speed, such as the earth. Individual points on the surface will move at different speeds, depending on whether they are closer to the pole or the equator. By using the cross product we can concisely define the speed at every point, it turns out it is given by $\Omega \times {\bf x}$, where $\Omega$ is the angular velocity of the earth and is a constant vector pointing along its axis, and ${\bf x}$ is the position vector from the centre of the earth to the point on the surface we're interested in.

The cross product is crucial in the physical sciences when using Moments. Moments allow us to calculate how an object, pivoted at a certain point, will move when a force is exerted upon it. Consider pushing a door. If the (shortest) vector from the hinge axis to the place where the door is pushed is ${\bf r}$, and the force exerted is ${\bf F}$, then the moment is ${\bf r} \times {\bf F}$, and is equal to the moment of inertia of the door (a property of the door) multiplied by the acceleration of the door around its axis, the hinge. This is a form of Newton's second law, Force = Mass x Acceleration. The further away from the hinge the door is pushed, the larger moment is exerted, and the faster the door moves.

New definitions and techniques:- Triple products, ${\bf a} \times {\bf b} \times {\bf c}$ and ${\bf a} \cdot {\bf b} \times {\bf c}$.
Vectors are useful for: Finding the shortest distance between two lines. Defining the Electromagnetic equations. And lots more.
Suggested NRICH problems: V-P Cycles; Flexi Quads; Flexi-Quad Tan
Further information - NRICH articles: Vectors - What Are They?; Multiplication of Vectors

2. Matrices

A Matrix is a way of concisely setting up several linear relationships at once, such as a system of simultaneous equations. These relationships may transform a vector $(x_0,y_0)$ to a new vector $(x_1,y_1)$ in a particular way, for example rotating the original vector by $\theta$ about the origin. Or the relationships may be a set of linear differential equations which we need to solve simultaneously.

You will have come across problems involving a single spring attached to a single mass (see Building Up Friction for an in-depth question) but now imagine a coupled system, such as a train with two carriages with connectors that can be modelled as springs (spring constants $k_1$ and $k_2$, unstretched lengths $L_1$ and $L_2$)

Say the train comes to a stop, and we are interested in the subsequent motion of the carriages. There are two degrees of freedom, $x_1$ and $x_2$, the positions of the two carriages. We find the following equations

$m_1 \ddot{x}_1 = - k_1 (x_1 - L_1) + k_2 (x_2 - x_1 -L_c - L_2)$

$m_2 \ddot{x}_2 = -k_2 (x_2 - x_1 - L_c - L_2)$

We can put this into matrix form

$ \left( \begin{array}{cc} m_1 & 0 \\ 0 & m_2 \end{array} \right) \left( \begin{array}{c} \ddot{x}_1 \\ \ddot{x}_2 \end{array} \right) + \left( \begin{array}{cc} k_1 + k_2 & -k_2 \\ -k_2 & k_2 \end{array} \right) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{c} k_1 L_1 - k_2(L_2 + L_c) \\ k_2 (L_2 + L_c) \end{array} \right)$

Or, more concisely

$M \ddot{X} + K X = F$

where $M$, $K$ and $F$ could be described as the mass, spring constant and forcing matrices respectively. We can now use matrix techniques to solve the problem.

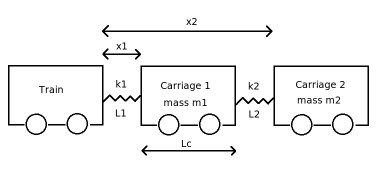
New definitions and techniques:- Eigenvectors and eigenvalues. Matrix multiplication. Inverse of a Matrix. Determinants.
Matrices are useful for: Physical systems with several degrees of freedom. Solving simultaneous equations. Writing mathematical expressions concisely.
Suggested NRICH problems: The Matrix; Fix Me or Crush Me; Transformations for 10

3. Complex numbers

When faced with a differential equation to solve, very often in the physical sciences you look for solutions of the form $e^{i \omega t}$, (where $t$ is the variable we are differentiating with respect to) and then solve for $\omega$. [Note that engineers often use $j$ for the square root of -1, rather than $i$, so as not to confuse it with the symbol for current.] This simplifies things considerably, as differentiating becomes equivalent to multiplication by $i \omega$. It also means undergraduates need to be very comfortable with manipulating complex numbers, and the

$e^{i \omega t} = \cos (\omega t) + i \sin (\omega t)$

formula.

So how do we know in advance that complex exponentials are a good idea for the solution to a given problem? In part, the answer is Fourier Theory (see below), which shows that any function (pretty much), can be re-expressed as a sum of exponentials. Basically, exponentials are the fundamental solutions to Linear Differential Equations, and all other solutions are made up of these building blocks.

New definitions and techniques:- $r e^{i \theta}$ notation. Complex roots. De Moivre's Theorem.

Complex numbers are useful for: Solving Linear Differential Equations in Electronics, Vibrations and Mechanics. See for example the article AC/DC Circuits. Fourier Series.

Suggested NRICH problems: The Not-so-simple Pendulum 2; Complex Sine

Further information: An Introduction to Complex Numbers; What Are Complex Numbers?; Curious Quaternions (Plus magazine)

4. Fourier Series

Fourier Series are a clever way of re-expressing a periodic function, $f(x)$, as a sum of sines and cosines. There's quite a nice graphical illustration of this for a square wave in the Wikipedia article on Fourier Series.

It is important to remember that sines and cosines are made up of exponentials (many people forget these useful relationships when doing problems - can you remember them?), and thus a Fourier Series is also a clever way of re-expressing a periodic function in terms of exponentials. Since exponentials are particularly easy to differentiate and integrate, by splitting a problem into lots of exponential components we can often solve differential equations which we couldn't solve with the original $f(x)$. Or there may be standard solutions for exponentials which someone else has previously worked out (this is where engineers' databooks come in handy).

Now the really clever bit is that usually in real life we are only interested in a limited range of $x$, and so we can 'pretend' a function is periodic when actually it isn't, by defining it outside the range of interest. Say we are only interested in $0< x< L$, we simply define $f(x) = f(x-L)$ for $x> L$ and, ta dah!, we have a periodic function.

New definitions and techniques:- Rate of convergence - how many terms of the Series will you need to get a good estimate for the original function?

Fourier Series are useful for: Solving Linear Systems, that is one or more linear differential equation. Re-expressing a function in terms of exponentials or sines/cosines.

5. Differential equations

A lot of undergraduate activity in the physical sciences is about constructing and solving Differential Equations (DEs). Often the hardest part of a question is writing down the correct equation from the wordy description you are given. If you haven't got the correct equation to begin with, solving it can prove impossible! Sign errors, such as confusing which direction a force is acting in, can lead to big problems. The way to eliminate these is practice and careful working, as well as thinking about whether the equation you have found makes sense (e.g. if you increase the force in the equation, will the system respond as you would expect from common sense?).

Techniques for solving differential equations are an important part of the physical scientist's tool box. You will probably have met in A-Level: Change of variables; Integrating factors; Separation of variables. New techniques used at university include:

Difference equations. These are often used in solving a system of equations when stepping forward in time. Instead of solving a DE to find a continuous function $f(t)$, where $t$ (time) can be any real number greater than zero, we seek $f$ at specific points in time, $f_1 = f(t_1)$ etc. This means we can write out a set of simultaneous equations to solve algebraically, instead of differential equations.

Convolution (also called Green's functions). Suppose we have a differential equation with some function $f(x)$ on the right hand side e.g.

$\frac{d^2y}{dx^2} + \alpha y = f(x)$

Convolution is a cunning way of finding $y(x)$ for any $f(x)$ just by working out what $y(x)$ would be if $f(x) = \delta(x - x_0)$. This involves another new mathematical idea you will learn about, delta functions. The delta function $\delta (x-x_0)$ represents an infinite spike at $x = x_0$, and although it seems rather an odd concept at first (a bit like imaginary numbers), it turns out to be incredibly useful.

Laplace Transforms and Fourier Transforms. As implied in Difference equations above, solving algebraic equations (e.g. $3 y^2 - 5 y = 0$) is usually much easier than solving equations involving derivatives. Applying a Transform to a DE means integrating the whole thing with respect to a completely new variable, (conventionally $k$ or $\omega$). This gives us a new equation to solve, where crucially any derivative terms from the original equation are now just algebraic terms, e.g. $\frac{d^2 y}{d x^2} \rightarrow - k^2 {\hat y}$. (${\hat y}$ is the new function we are now solving for). Clever stuff.

Differential equations are good for: Modelling physical systems.
Suggested NRICH problems: Differential Electricity; Euler's Buckling Formula; Ramping it Up

Related Collections

More university preparation

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Maths in the Undergraduate Physical Sciences

1. Vector manipulation

2. Matrices

3. Complex numbers

4. Fourier Series

5. Differential equations

Related Collections

You may also like

Overarch 2

Stonehenge

Maximum Flow