Skip over navigation
Here is a man among the trees looking at where to put a fence. It's a circular fence.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
It's a Fence!
Age 5 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
It's a Fence!
Here is a man among the trees looking at where to put a fence. It's a circular fence.

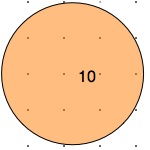
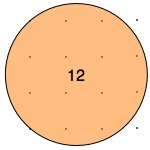
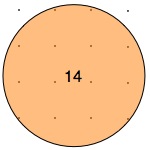
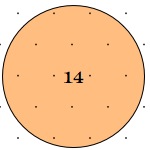
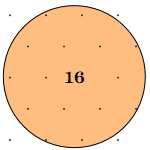
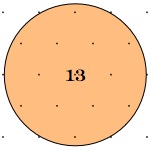
These diagrams show where the fence may go when the trees are planted in squares:



These diagrams show where the fence may go when the trees are planted in triangles:



So, let's start by looking at different examples of these circles and see what things we notice. Then we could decide what we could try out and explore!
This problem could be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
Why do this problem?
There are many ways of approaching this problem, so pupils with different ways of thinking and working can all contribute. Some experience of speaking and listening effectively with others would be of benefit.
The problem lends itself to collaborative working, both for children who are inexperienced at working in a group and children who are used to working in this way. By working together on this problem, the task is shared and therefore becomes more manageable than if working alone.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This is an ideal problem for learners to tackle in groups of two then four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task could be measured by
how effectively members of the group work together as well as by their final solution. This version of the roles has been adapted for primary children. You may want to alter the names of the roles for young children, but on the other hand, many may enjoy
getting to grips with important-sounding titles!
Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
One way of working would be to have the pupils working in pairs. The first pair of children could then be given the "circular fences around trees arranged in squares" images and the second pair be given the "circular fences around trees arranged in triangles" images, both of which can be printed off from here: Word, pdf. After a while first pairs could join the second pairs to form a team of four and compare what they think. They could then come up with an agreed question to pursue. When the groups of four pupils have had some time to work further, these other images
(Word, pdf) of squares and triangles could just be shown with the simple question, "What do you think?".
Key questions
Discussion could be initiated if necessary by asking,
"What do you think about the numbers?"
"Would you think of other numbers?" and "What would they be?"
Ask learners to identify which skills they demonstrated, and which skills they need to develop further; or ask them to identify someone else in the group who demonstrated a particular skill.
If your focus is mathematical, these questions may be appropriate:
What can you say about the circles and trees represented as dots?
Possible extension
Try other shapes of fences. There are some pentagons here in case you'd like to try those.
Possible support
Sheets of dotty paper (squared and triangular) will be very helpful for this activity. You may need to support some children at the start of the discussions in groups.
You may also like
Baked Bean Cans
Is there a best way to stack cans? What do different supermarkets do? How high can you safely stack the cans?

