Skip over navigation
Class 5AM from St Peter's School, Barcelona, worked on this problem in groups. Here is their report.
Yusuf from Columbia Primary School told us:
We made our cubes using modular origami. We had to measure each piece of paper to make sure it was the correct size and that it would make the right sized cube. We worked out the volume of each cube and wrote it on the side.
Kathy and Pete from Barley Hill Primary School decided to see what patterns they could find by making cuboids.
First we drew the nets of our cuboids.
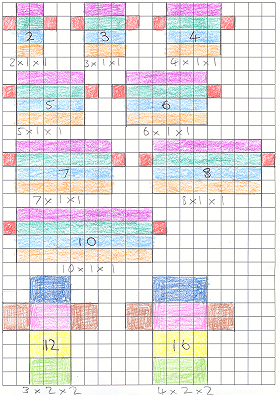
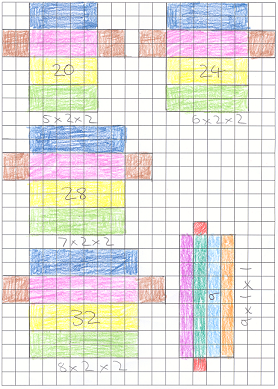
We noticed that the volume of our first set where we just added one square to the length of the rectangle went up by $1$ each time. The volume of our second set went up by $4$ each time. This is different to the set of cubes in the problem which went up different amounts each time because we only changed one length of our shape.
Here is a picture of their graded cuboids.
Well done for sending in your pictures.
There are lots more shapes you could make - you could see what happens to the volume if you change more than one side of a cuboid.
Next Size Up
Age 7 to 11
Challenge Level 
Class 5AM from St Peter's School, Barcelona, worked on this problem in groups. Here is their report.
Yusuf from Columbia Primary School told us:
We made our cubes using modular origami. We had to measure each piece of paper to make sure it was the correct size and that it would make the right sized cube. We worked out the volume of each cube and wrote it on the side.
Kathy and Pete from Barley Hill Primary School decided to see what patterns they could find by making cuboids.
First we drew the nets of our cuboids.
We noticed that the volume of our first set where we just added one square to the length of the rectangle went up by $1$ each time. The volume of our second set went up by $4$ each time. This is different to the set of cubes in the problem which went up different amounts each time because we only changed one length of our shape.
Here is a picture of their graded cuboids.
Well done for sending in your pictures.
There are lots more shapes you could make - you could see what happens to the volume if you change more than one side of a cuboid.
You may also like
Castles in the Middle
This task depends on groups working collaboratively, discussing and reasoning to agree a final product.
Which Solid?
This task develops spatial reasoning skills. By framing and asking questions a member of the team has to find out what mathematical object they have chosen.
Triple Cubes
This challenge involves eight three-cube models made from interlocking cubes. Investigate different ways of putting the models together then compare your constructions.