Triple Cubes

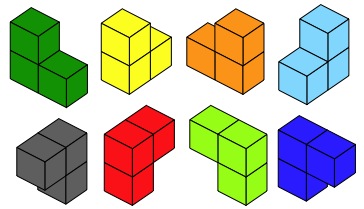
Well, here I've placed a group of cubes. They are in threes and coloured differently.

 

What do you notice about them?

 

You could get $8$ triple cubes like these, each triple a different colour. Don't separate the triple but use them as building blocks to see what you can make.

 

For some of you it would be good to keep the eight triple cubes facing their own ways and not turn them around. In this way we keep eight arrangements that are different.

 

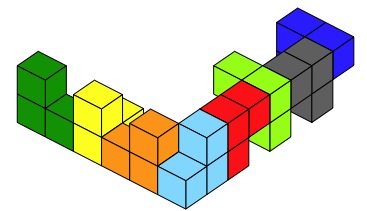
We can now use these as building blocks to make interesting arrangements and shapes. Here is one to start us off.

 

Notice how I've joined them together with square faces touching. This might be the way that you decide to build.

 

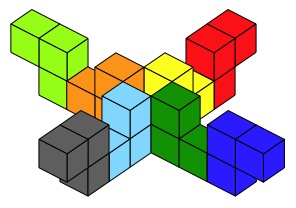
Or, you may include some "edge" joining as in this one.

 

 

So now it's your turn to see what you can make from these eight triple cubes.