Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Attractive Rotations



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to Sally and Emily from Parrs Wood for sending us pictures of their rotations. Here are their findings.
Sally noticed a pattern with the coordinates of our shape.
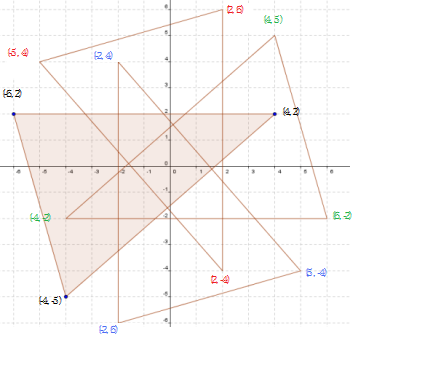
In the table below, the coordinates (x',y') describe where the points (x,y) end up after they have rotated by $90^\circ$ around (0,0):
| (x,y) | (x',y') |
| (-4,-5) | (-5,4) |
| (-6,2) | (2,6) |
| (4,2) | (2,-4) |
| (-5,4) | (4,5) |
| (2,6) | (6,-2) |
| (2,-4) | (-4,-2) |
| (4,5) | (5,-4) |
| (6,-2) | (-2,6) |
| (-4,-2) | (-2,4) |
| (5,-4) | (-4,5) |
| (-2,6) | (2,-6) |
| (-2,4) | (4,2) |
So the coordinates (x',y'), which are a rotation of (x,y) by $90^{\circ}$ around (0,0), are (y, -x).
$180^{\circ}$ rotation is just two $90^{\circ}$ rotations so
(x,y) $\longrightarrow$ (x',y') = (y,-x) $\longrightarrow$ (y',-x') = (-x, -y).
$90^{\circ}$ $90^{\circ}$

I predicted rotations of $30^{\circ}$ would have rotational symmetry of order 12 and $72^{\circ}$ would have rotational symmetry of order 5 because $360\div30 = 12$ and $360\div72 = 5$. These were true for the pictures I drew. I also knew I couldn't colour in my $72^{\circ}$ rotation shape because 5 is prime so its only factors are 5 and 1.
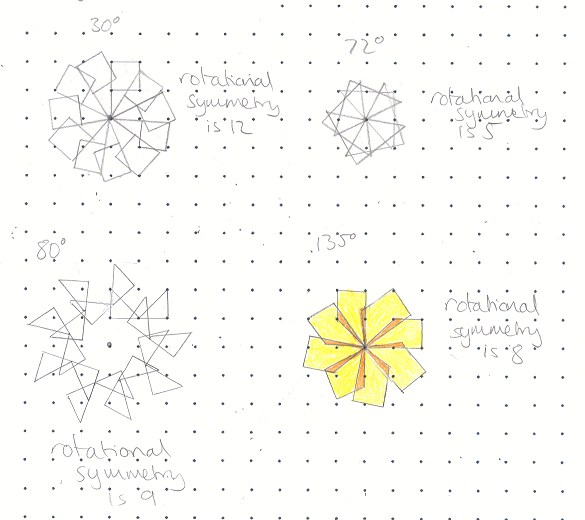
$360\div80 = 4.5$ and I had to go round twice to complete my shape. This then gave me rotational symmetry of order 9 because $360\times2=720$ and $720\div80 = 9$.
As $360\div135 = 2{2\over3}$, I worked out $360\times3=1080$ and $1080\div135 = 8$ so I knew I had to go round 3 times to get a shape with rotational symmetry.
Mr Bakker sent us a photo of the work some of his students did on this task:

Do continue sending us pictures of your rotation patterns along with any interesting mathematical discoveries you make.
You may also like
Illusion
A security camera, taking pictures each half a second, films a cyclist going by. In the film, the cyclist appears to go forward while the wheels appear to go backwards. Why?
Weighty Problem
The diagram shows a very heavy kitchen cabinet. It cannot be lifted but it can be pivoted around a corner. The task is to move it, without sliding, in a series of turns about the corners so that it is facing the other way round.
Rolling Triangle
The triangle ABC is equilateral. The arc AB has centre C, the arc BC has centre A and the arc CA has centre B. Explain how and why this shape can roll along between two parallel tracks.

