Skip over navigation
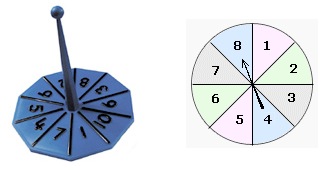
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the "tens" figure and the other one for the "units" (or "ones").
Our Numbers
Age 5 to 7
Challenge Level 
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the "tens" figure and the other one for the "units" (or "ones").
You will need two spinners like those above and two cards which each have six boxes drawn on them. You can download and print these, or you could use our interactive spinners. You will also need twelve counters.
A person with one card chooses the special types of numbers that they will collect. The other person chooses some other special types of numbers to collect.
For example, Sara chooses numbers you can share equally among $3$ ( eg. $3, 9, 21, 39 ... $).
Nala chooses even numbers (eg. $4, 10, 20, 44 ... $).
Each of them spins a spinner and then when it rests they read out the number (tens and units).
Suppose it's a $21$ then Sara places a counter in one of the boxes on her card. If it is a $10$ then Nala gets a counter for her card. If it's a $30$ then both of them get a counter.
So you can do something similar.
When you've tried it a few times decide what's best to choose so that you fill all the boxes on both cards as quickly as you can.
Think about other spinners - there are some here. Or of course you can design your own.
Are there good choices of spinners that work really well?
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
