Skip over navigation
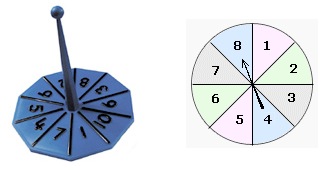
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the "tens" figure and the other one for the "units" (or "ones").
Our Numbers
Age 5 to 7
Challenge Level 
Our Numbers
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the "tens" figure and the other one for the "units" (or "ones").
You will need two spinners like those above and two cards which each have six boxes drawn on them. You can download and print these, or you could use our interactive spinners. You will also need twelve counters.
A person with one card chooses the special types of numbers that they will collect. The other person chooses some other special types of numbers to collect.
For example, Sara chooses numbers you can share equally among $3$ ( eg. $3, 9, 21, 39 ... $).
Nala chooses even numbers (eg. $4, 10, 20, 44 ... $).
Each of them spins a spinner and then when it rests they read out the number (tens and units).
Suppose it's a $21$ then Sara places a counter in one of the boxes on her card. If it is a $10$ then Nala gets a counter for her card. If it's a $30$ then both of them get a counter.
So you can do something similar.
When you've tried it a few times decide what's best to choose so that you fill all the boxes on both cards as quickly as you can.
Think about other spinners - there are some here. Or of course you can design your own.
Are there good choices of spinners that work really well?
Why do this problem?
This problem gives pupils the opportunity to use all their number knowledge and expand their number awareness. There is a chance to experience an element of scientific exploration as they choose the properties of the two groups and test to see what happens.
Possible approach
Have two spinners ready to generate the tens and units figures, and then with the class decide on two different groups (sets) of numbers to look out for. (You could make your own spinners or use our interactive versions.) When a number is generated this gives an opportunity for discussion about which group the number belongs to - if
any.
When this introduction has been repeated a number of times with different sets being chosen, discuss with the pupils about what affects the choices of sets so as to get six of each set in as few spins as possible. Give them chance to try out their own combinations in pairs.
Allow time for the whole group to come together to talk about the combinations they tried and to report on their findings. This might also be a good time for children to pose further questions which they would like to investigate.
Key questions
Tell me about the group you've chosen.
Can you say something about why you made this choice.
How do you decide whether the spinners' number belongs to your choice?
Possible extension
Some children could make hundreds, tens and units spinners.
For a further challenge, learners could design some different spinners - what about ones that contain just some of the numbers twice? How does this affect the children's choice of numbers?
Possible support
The children may need some adult support to physically spin the spinners. Some may need help in remembering how to check whether the number belongs to their group.
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
