Skip over navigation
This game is for two players, and you will need paper and a pencil.
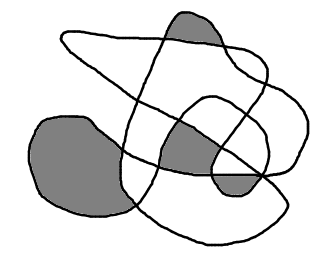
Start by drawing a curve on the paper. The curve can cross over itself as many times as you like, but must join back to where you started (this is called a closed curve).
Here is an example of the sort of curve you might draw:
Colouring Curves Game
Age 7 to 14
Challenge Level 
This game is for two players, and you will need paper and a pencil.
Start by drawing a curve on the paper. The curve can cross over itself as many times as you like, but must join back to where you started (this is called a closed curve).
Here is an example of the sort of curve you might draw:
Now take it in turns to
choose a region and colour it in. The only rule is that shaded
regions can't share an edge, although it's ok for them to meet at a
corner or vertex.
This is what the curve above might look like after each player has
had two turns:Eventually, you will run
out of regions to shade without shading regions which share an
edge. The last person who can shade a region is the winner!
Here are some ideas to think about as you play:
- Is it better to go first or second? Does it depend on the curve?
- Can you design some simple curves where you can guarantee that you will win?
- What do you notice about the number of regions that meet at each vertex?
- Can you come up with any strategies to help you to win?
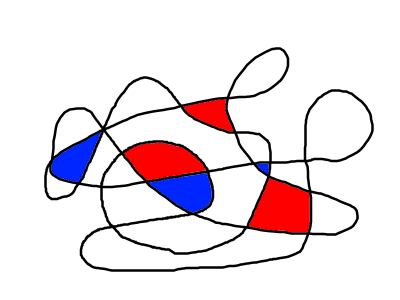
Another way to play the
game is to take it in turns to shade regions each using a different
colour, without shading adjacent regions in your own colour, so the
game might look a bit like this:
You may also like
Flow Chart
The flow chart requires two numbers, M and N. Select several values for M and try to establish what the flow chart does.