Skip over navigation
Colouring Curves Game
Age 7 to 14
Challenge Level 
Why play this game?
This game provides an opportunity for learners to consider strategy and thinking ahead. Playing the game could provide a starting point for reading about mathematical ideas such as the Four Colour Theorem.Possible approach
The game works well when
played in pairs. Learners could use pencil and paper, or perhaps
whiteboards. Once everyone has had the chance to play the game a
few times, the class could discuss any strategies they came up with
and explain anything they noticed while playing the game.
If learners play the two
colour version described at the end of the problem, they could
create some intriguing images for classroom display.
Key questions
Is it better to go first or second? Does it depend on the curve?Can you design some
simple curves where you can guarantee that you will win?
What do you notice about
the number of regions that meet at each vertex?
Can you come up with any
strategies to help you to win?
Possible extension
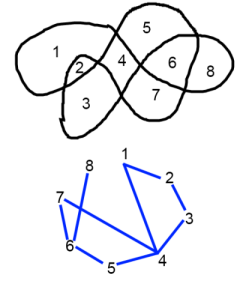
The game could be
investigated using various different representations for the curves
- one example is a graph such as this:
By using the rule that no
two connected numbers can be coloured the same, learners could
experiment with different curves and investigate the idea that all
such curves can be coloured with just two colours.
Further investigation of
these ideas at a higher level can be found in the Stage 5 problem
Painting by
Numbers.
Possible support
Start with some very simple curves with a small number of regions and work on the problem of how to decide whether to go first or second.You may also like
Flow Chart
The flow chart requires two numbers, M and N. Select several values for M and try to establish what the flow chart does.