Population Dynamics - Part 3

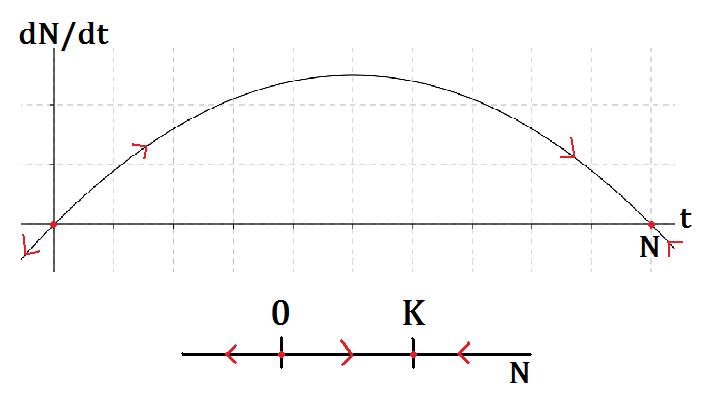
We first solve this equation:

$$\begin{align*} \frac{\mathrm{d}N}{\mathrm{d}t}&=rN(1-\frac{N}{K}) \\ \frac{1}{K} \frac{\mathrm{d}N}{\mathrm{d}t} &= \frac{N}{K} r(1-\frac{N}{K}) \end{align*}$$ To simplify this, let $x=\frac{N}{K}$ $$\begin{align*} \frac{\mathrm{d}x}{\mathrm{d}t}&=xr(1-x) \\ \frac{\mathrm{d}x}{x(1-x)}&=r\mathrm{d}t \\ \Big( \frac{1}{x}+\frac{1}{1-x} \Big) \mathrm{d}x&=r\mathrm{d}t \\ ln\Big(\frac{x}{1-x}\Big)&=rt+c \\ \frac{x}{1-x}&=X_0e^{rt} \\ x&=X_0e^{rt}-x X_0e^{rt} \\ x&=\frac{X_0e^{rt}}{1+X_0e^{rt}} \end{align*}$$ Putting N back in: $$N(t)=\frac {K N_0 e^{rt}}{K+N_0 (e^{rt}-1)}$$ As expected, over time the population tends to the maximum allowed by the environment: $$\lim_{t\to\infty} N(t)=K$$