Skip over navigation
Pour 2$^{ème}$ cycle de l'élémentaire
Matériel
Une grille de 100
Environ 100 jetons
Partie A
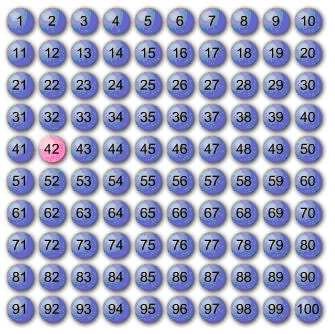
Marc et Safia ont une grille de 100.
Ils ont placé un jeton sur 42.
Pour essayer la version électronique de cette activité, allez à Where Can We Visit?.
Ils se demandent s'il est possible de couvrir tous les nombres de la grille en faisant deux opérations seulement : fois 2 et moins 5.
Ils ont commencé ainsi : 42, 37, 32, 27, 22, 17, 12, 7, 14, 9, 18, 13, 26, 52, 47, 42, 84 ...
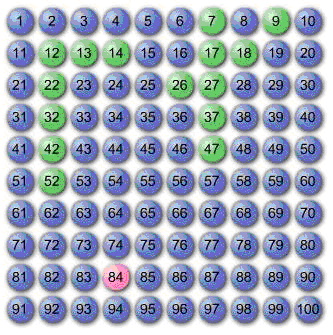
Il est permis de visiter le même nombre plus d'une fois. Le tableau de droite représente les nombres visités.
Sera-t-il possible de visiter tous les nombres?
Que se passerait-il s'ils avaient commencé avec un nombre différent de 42?
Pouvez-vous expliquer ces résultats?
Partie B
Marc et Safia se sont demandés s'ils obtiendraient la même sorte de réponses s'ils avaient choisi une paire d'opérations différentes.
Ils ont essayé :
fois 3 et moins 5
fois 4 et moins 5
fois 5 et moins 5
Ensuite, ils ont essayé :
fois 5 et moins 2
fois 5 et moins 3
fois 5 et moins 4
Qu'est-ce que Marc et Safia ont découvert?
Pouvez-vous expliquer les résultats?
Extension
Choisis un point de départ et une paire d'opérations et détermine ce qui arrive.
Source: Where Can We Visit?
Translated by Renée Michaud, Coordonnatrice et consultante de mathématiques et sciences, Consortium provincial francophone pour le perfectionnement professionnel, Calgary, Canada
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Où Irons-nous?
Age 7 to 11
Challenge Level 





- Problem
- Teachers' Resources
Pour 2$^{ème}$ cycle de l'élémentaire
Matériel
Une grille de 100
Environ 100 jetons
Partie A
Marc et Safia ont une grille de 100.
Ils ont placé un jeton sur 42.

Pour essayer la version électronique de cette activité, allez à Where Can We Visit?.
Ils se demandent s'il est possible de couvrir tous les nombres de la grille en faisant deux opérations seulement : fois 2 et moins 5.
Ils ont commencé ainsi : 42, 37, 32, 27, 22, 17, 12, 7, 14, 9, 18, 13, 26, 52, 47, 42, 84 ...

Il est permis de visiter le même nombre plus d'une fois. Le tableau de droite représente les nombres visités.
Sera-t-il possible de visiter tous les nombres?
Que se passerait-il s'ils avaient commencé avec un nombre différent de 42?
Pouvez-vous expliquer ces résultats?
Partie B
Marc et Safia se sont demandés s'ils obtiendraient la même sorte de réponses s'ils avaient choisi une paire d'opérations différentes.
Ils ont essayé :
fois 3 et moins 5
fois 4 et moins 5
fois 5 et moins 5
Ensuite, ils ont essayé :
fois 5 et moins 2
fois 5 et moins 3
fois 5 et moins 4
Qu'est-ce que Marc et Safia ont découvert?
Pouvez-vous expliquer les résultats?
Extension
Choisis un point de départ et une paire d'opérations et détermine ce qui arrive.
Source: Where Can We Visit?
Translated by Renée Michaud, Coordonnatrice et consultante de mathématiques et sciences, Consortium provincial francophone pour le perfectionnement professionnel, Calgary, Canada

