Skip over navigation
Four identical robots and their enemies, the stick men, live in small universes based on squares with the opposites sides identified (i.e. corresponding to the same points in space) in various ways, as shown in the diagrams below:
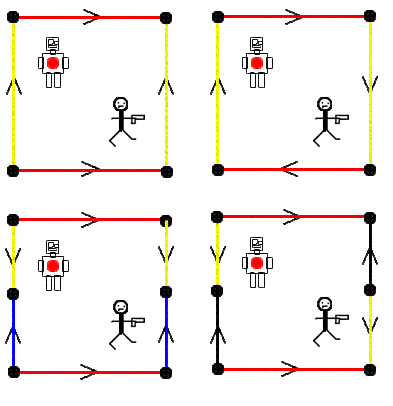
Consider these universes. In which ways could the stick men shoot the robots? Which create a geometry which can be made in 3 dimensions out of a sheet of paper? Perhaps you might like to experiment with other universes?
Weird Universes
Age 16 to 18
Challenge Level 
Four identical robots and their enemies, the stick men, live in small universes based on squares with the opposites sides identified (i.e. corresponding to the same points in space) in various ways, as shown in the diagrams below:
Consider these universes. In which ways could the stick men shoot the robots? Which create a geometry which can be made in 3 dimensions out of a sheet of paper? Perhaps you might like to experiment with other universes?
Did you know ... ?
String theory suggests that each point we see in 3D space is in fact a higher dimensional surface wrapped up in very specific ways.
String theory suggests that each point we see in 3D space is in fact a higher dimensional surface wrapped up in very specific ways.
You may also like
Euler's Formula
Some simple ideas about graph theory with a discussion of a proof of Euler's formula relating the numbers of vertces, edges and faces of a graph.
Air Nets
Can you visualise whether these nets fold up into 3D shapes? Watch the videos each time to see if you were correct.
Stereoisomers
Put your visualisation skills to the test by seeing which of these molecules can be rotated onto each other.