Area and Perimeter
What can you say about these two shapes?
What can you say about the shapes below?
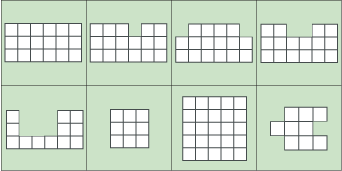
Can you draw a shape in which the area is numerically equal to its perimeter? And another?
Can you draw a shape in which the perimeter is numerically twice the area?
Can you draw a shape in which the area is numerically twice the perimeter?
Can you make the area of your shape go up but the perimeter go down?
Can you make the perimeter of your shape go up but the area go down?
Can you draw some shapes that have the same area but different perimeters?
Can you draw some shapes that have the same perimeter but different areas?
You may also like
Shaping It
These pictures were made by starting with a square, finding the half-way point on each side and joining those points up. You could investigate your own starting shape.
Cylinder Cutting
An activity for high-attaining learners which involves making a new cylinder from a cardboard tube.