Skip over navigation
Tom and Ben were in Numberland in the county of Addition.
They had a map which looked like this:
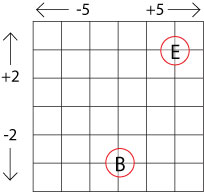
They were at point B and they began their journey with ten points.
For every square they walk to the right on the map, they add five.
For every square they walk to the left on the map, they take away five.
If they go North (up on the map), they added two for every square, and if they go South (down on the map), they take away two for each square.
First they made these journeys:
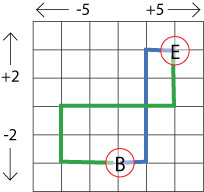
The blue line shows Tom's journey and the green line shows Ben's.
How many points did they have each when they reached E?
Do you notice anything?
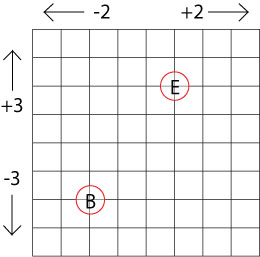
Here is a different grid for you to make up some journeys of your own, beginning at B and ending at E.
After they had explored in the county of Addition in Numberland, Tom and Ben went on to the county of Multiply.
Here they had a new map which looked like this (here are two copies of the map):
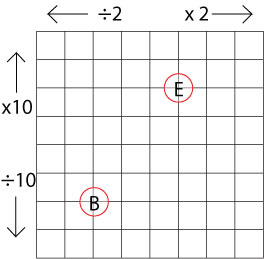
They explored here too. Each time they started at B with $10$ points and made their way to E. Try lots of journeys yourself.
What do you notice about the journeys this time?
Can you explain why this happens?

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Journeys in Numberland
Age 7 to 11
Challenge Level 





Tom and Ben were in Numberland in the county of Addition.
They had a map which looked like this:

They were at point B and they began their journey with ten points.
For every square they walk to the right on the map, they add five.
For every square they walk to the left on the map, they take away five.
If they go North (up on the map), they added two for every square, and if they go South (down on the map), they take away two for each square.
First they made these journeys:

The blue line shows Tom's journey and the green line shows Ben's.
How many points did they have each when they reached E?
Do you notice anything?
Here is a different grid for you to make up some journeys of your own, beginning at B and ending at E.

You can download and print off this sheet which has two copies of the grid map.
What do you notice about your different journeys?
Can you explain your observations?
After they had explored in the county of Addition in Numberland, Tom and Ben went on to the county of Multiply.
Here they had a new map which looked like this (here are two copies of the map):

They explored here too. Each time they started at B with $10$ points and made their way to E. Try lots of journeys yourself.
What do you notice about the journeys this time?
Can you explain why this happens?
You may also like
Follow the Numbers
What happens when you add the digits of a number then multiply the result by 2 and you keep doing this? You could try for different numbers and different rules.
Triple Cubes
This challenge involves eight three-cube models made from interlocking cubes. Investigate different ways of putting the models together then compare your constructions.
Inky Cube
This cube has ink on each face which leaves marks on paper as it is rolled. Can you work out what is on each face and the route it has taken?

