Skip over navigation
The dice has been rolled around without sliding, and it has printed the picture below. Your challenge is to find where the cube was placed to begin with and map out the route it has travelled. You may find it useful to print off a copy of the picture on this sheet.
There are two different ways of arranging the numbers on the faces of dice. If you look at the faces '1', '2' and '3' on a dice, you can see that they share a vertex. In a left-handed dice, the '1', '2' and '3' run clockwise, and in a right-handed dice they go anti-clockwise. See Right or Left? for more information about this. If you're using a dice for this activity, first work out which type of dice you have and then use the matching print below.
Right-handed dice print:
Rolling That Cube
Age 5 to 11
Challenge Level 
We have a dice with raised spots, which have been pressed on an ink pad.
We start by printing one number.
Can you see how the numbers below have been printed by rolling the dice in the four different directions?
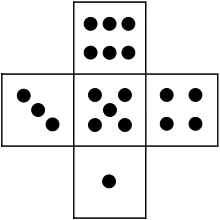
We start by printing one number.
Can you see how the numbers below have been printed by rolling the dice in the four different directions?
The dice has been rolled around without sliding, and it has printed the picture below. Your challenge is to find where the cube was placed to begin with and map out the route it has travelled. You may find it useful to print off a copy of the picture on this sheet.
There are two different ways of arranging the numbers on the faces of dice. If you look at the faces '1', '2' and '3' on a dice, you can see that they share a vertex. In a left-handed dice, the '1', '2' and '3' run clockwise, and in a right-handed dice they go anti-clockwise. See Right or Left? for more information about this. If you're using a dice for this activity, first work out which type of dice you have and then use the matching print below.
Right-handed dice print:
Left-handed dice print:
NB You may find that the six and two are in a different orientation when you try this out with your own right-handed or left-handed dice.
You may also like
Plants
Three children are going to buy some plants for their birthdays. They will plant them within circular paths. How could they do this?
Triangle Animals
How many different ways can you find to join three equilateral triangles together? Can you convince us that you have found them all?
Junior Frogs
Have a go at this well-known challenge. Can you swap the frogs and toads in as few slides and jumps as possible?